Parametrização Geométrica

Bem, vamos dar continuidade ao nosso estudo, mas agora abordando questões sobre a melhor forma de representarmos um perfil aerodinâmico. Como você faria esta representação? Através de um arquivo de pontos, um desenho CAD ou uma equação analítica? Bem, a melhor escolha depende do que se pretende analisar ou estudar.

Interessante, mas não entendi!

Veja, se você pretende executar simulação numérica ou realizar um ensaio em túnel de vento para avaliar um determinado perfil aerodinâmico, então, um arquivo de pontos ou um desenho CAD pode ser uma representação adequada. Visto que, a geometria está definida e o foco está em levantar às características aerodinâmicas da mesma e não em realizar alterações na geometria.

        Simulação Numérica

Túnel de Vento

Agora se você pretende fazer um estudo de otimização, então, uma equação analítica para definir o perfil aerodinâmico em função de parâmetros de entrada, como por exemplo, os coeficientes de um polinômio, pode ser a melhor representação. Repare que em um estudo de otimização várias geometrias deverão ser geradas e analisadas, sendo que, quando maior o número de variáveis de entrada do seu polinômio mais custoso se torna o processo de otimização. Isso será visto mais a frente, mas neste meio tempo guarde esta informação.

Certamente também é possível obter de maneira automática variações geométricas em um perfil ou asas através de uma ferramenta CAD. Porém, tem-se uma complexidade maior, visto que, o software de CAD escolhido precisará estar integrado no seu processo de otimização. Esta complexidade a mais pode ser pelas questões de licenças do CAD ou pelo simples fato de termos um custo maior de input/output no ambiente de otimização.

Quiz: Você acha que uma abordagem em que se modifica o perfil mexendo ponto por ponto parece algo razoável para um processo de otimização?

Vamos seguir adiante continuando com a ideia apresentada sobre um estudo de otimização para um perfil aerodinâmico. Existe diferentes abordagem para parametrizar a geometria do perfil. Entre estas possíveis parametrizações podemos citar:

• Curvas de Bézier
• Class and Shape Function Transformation – CST
• Parsec
• NURBS

Para dar prosseguimento com o raciocínio sobre um processo de otimização, as curvas de Bézier serão aqui adotadas. Neste ponto faz-se necessário entrarmos um pouco no equacionamento matemático, pois a ideia é que você comece a se familiarizar com aspectos que envolvem a parametrização geométrica.  O equacionamento das curvas de Bézier é representado pelas duas equações abaixo.

Onde, Bx(t) e By(t) representam os sucessivos pares (x,y) das coordenadas da geometria que se está gerando a partir dos pontos de controle. O termo b_i,n é o polinômio de Berstein que é dados pela equação abaixo, já o índice ‘n’ é a ordem do polinômio e o índice ‘i’ é valor corrente do somatório. O termo ‘t’ consiste em um determinado valor do vetor de pontos que foi gerado dentro do intervalo [0,1].

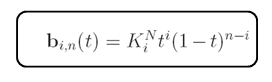
O termo K é o coeficiente binomial.

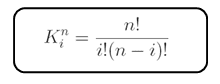
Bem, olhando as expressões acima se tem a impressão de algo complexo e este sentimento continuará até que você gaste 5 minutos para pensar em com seria a implementação computacional destas equações. Para ajudar vou descrever o desdobramento do equacionamento para um exemplo que está disponível em um arquivo Excel.

Espero que tenha ficado mais claro como se desdobra a formulação nestas duas equações para a coordenada X e Y dos pontos, que são dados por Bx(t) e By(t).

A imagem abaixo mostra o exemplo fornecido na planilha Excel. Altere as coordenadas (x,y) de um dos pontos de controle e veja como a geometria se altera. Para que você possa notar as alterações geométricas de maneira sequenciada mexa em um ponto de controle de cada vez.

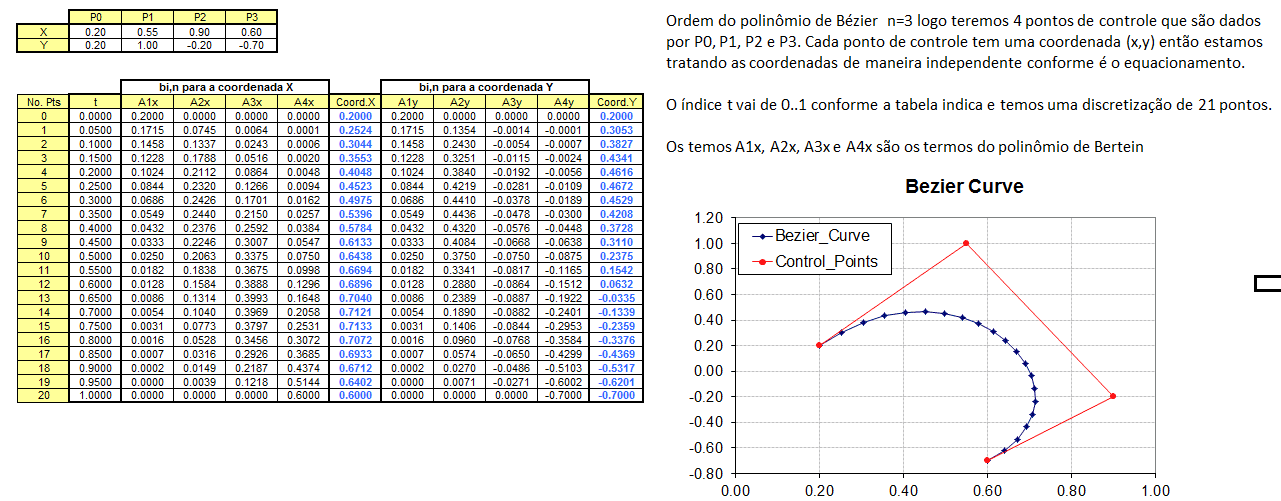
Bem, acredito que após as explicações acima você ganhou um pouco de familiaridade com o conceito das curvas de Bézier, certo? Mas como posso usar este conceito no dia a dia? Vamos ver alguns exemplos abaixo.

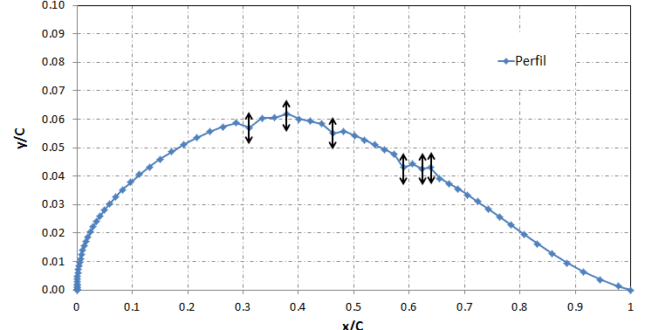
A figura abaixo mostra a curva de arqueamento e a curva de espessura relativa para o NACA2412 (2% de arqueamento máximo, localizado em 40% da corda e com espessura relativa de 12%). Os pontos que se encontram em torno destas duas curvas representam as coordenadas (x,y) dos pontos de controle de uma curva de Bézier que reproduz exatamente as duas curvas originais. Ou seja, a partir destes pontos de controle é possível restituir as curvas de arqueamento e espessura relativas ao NACA2412. Ok, mas por que eu quero achar os pontos de controle que me geram uma geometria que eu já tenho?

Bézier Curve – Control Points Definition

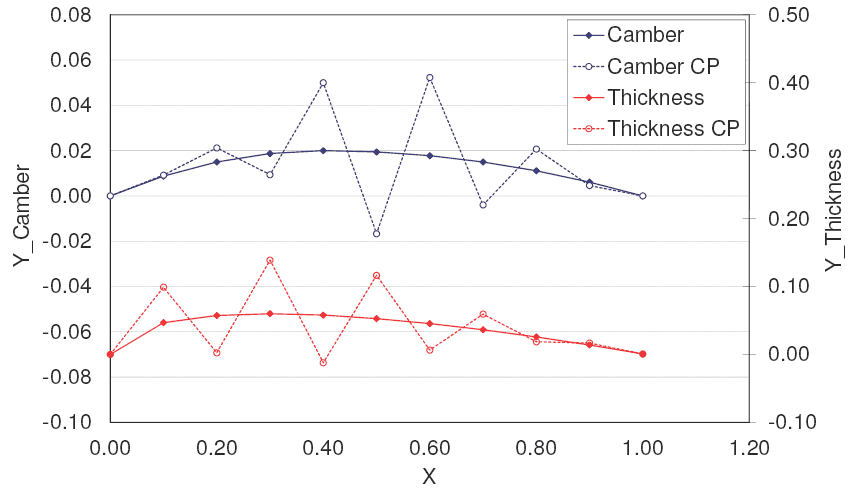
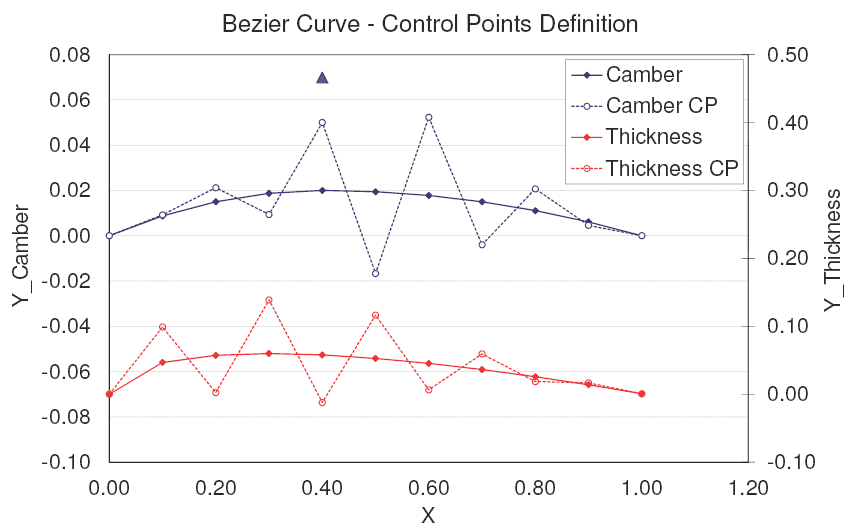
Bem, se você tem um perfil com uma determinada característica aerodinâmica que você deseja e gostaria de estudar o efeito de pequenas variações na geometria deste perfil, esta abordagem pode ser interessante. Vamos pegar como exemplo um perfil laminar ‘XYZ’ que é adotado na asa da sua aeronave para a competição do Aero Design, e por alguma razão construtiva você precisa alterar este perfil em uma dada seção da asa. Neste caso em específico, esta abordagem te permite fazer algumas análises de sensibilidade para achar a melhor solução de compromisso. A figura abaixo mostra uma alteração na coordenada y do quinto ponto de controle, contando da esquerda para direita o quinto círculo aberto passa a ter a posição indicada pelo triângulo cheio. Como consequência tem-se uma alteração na geometria do perfil.

A figura abaixo mostra o efeito da modificação no ponto de controle sob a geometria.

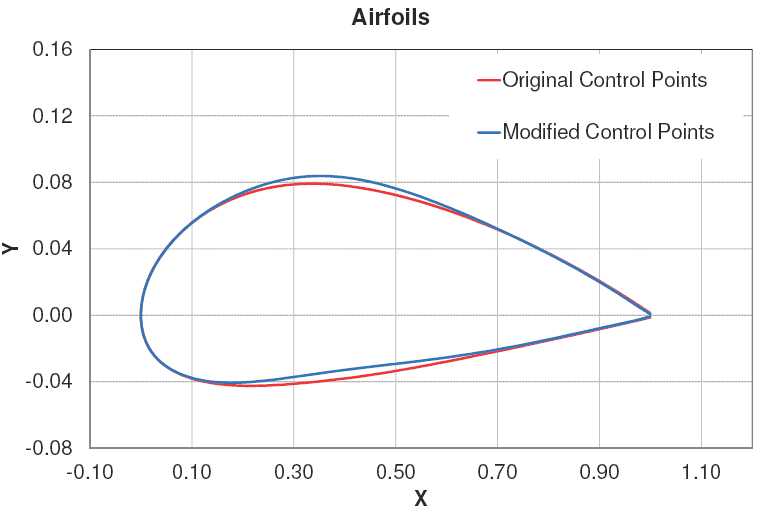
Neste ponto vamos usar o programa fornecido abaixo para gerar um perfil aerodinâmico a partir de pontos de controle que definem o extradorso (parte de cima) e o intradorso (parte de baixo) do perfil. Aqui estão alguns detalhes para que você possa usar este programa. Leia com atenção!

1. O código foi implementado na linguagem Python 3.0, então, você precisará instalar este programa no seu computador.

Além do Python será necessário o módulo do MatPlotlib para que você possa visualizar as figuras. Note que em algumas instalações do Python como a distribuição do ANACONDA, o pacote Matplotlib já está presente. Para quem não tiver familiaridade com o Python sugiro ver o vídeo do link a seguir para que possa executar a instalação do ANACONDA. https://www.youtube.com/watch?v=GPIScYdZqW0

2. Após instalar o pacote abrir o Spyder na janela iniciar do Windows.

Após a abertura da interface do Spyder abrir o código (Bezier_Upper_Lower.py) e executar o programa.

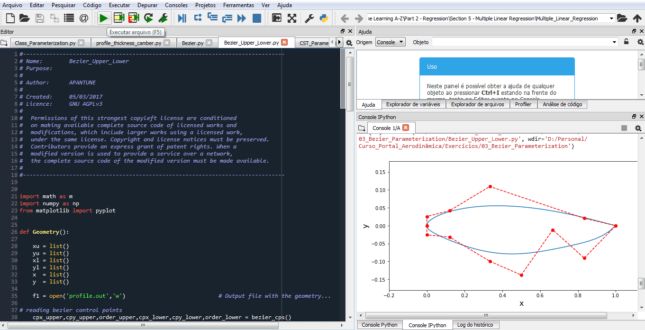
3. Este código lê dois arquivos de entrada: inp e cp_lower.inp.

4. O número de pontos de controle do extradorso (parte superior) e intradorso (parte inferior) do perfil não precisam ser os mesmos, mas é importante que no bordo de fuga e bordo de ataque eles sejam coincidentes para termos continuidade no perfil aerodinâmico. Sugestão não mexa na coordenada do primeiro e último ponto de controle. No segundo ponto de controle mexa apenas a coordenada Y. Já os demais pontos de controle estão livres para você poder alterar da forma que quiser, inclusive tirando ou adicionando novos pontos de controle. Não deixe linhas em branco após o último ponto de controle! Isso fará com que o programa dê um ‘crash’ pois o mesmo lerá um ponto de controle nulo!

5. Mantenha a primeira linha dos arquivos de entrada. O resultado da geometria gerada está no arquivo out

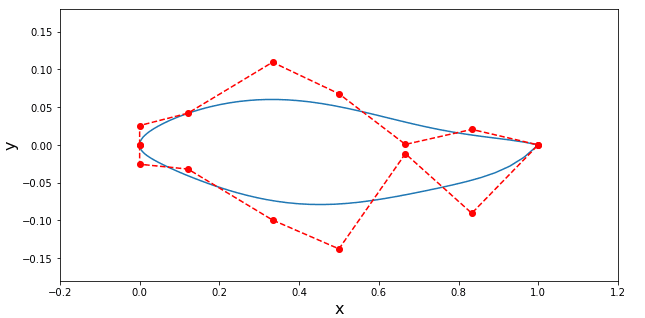
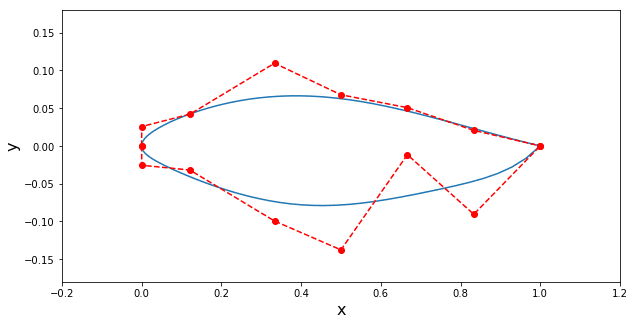
As figuras abaixo mostram um exemplo dos arquivos de entrada e os pontos de controle e a geometria criada. A primeira figura mostra a geometria para os dados que estão sendo disponibilizados, já a segunda mostra para a alteração no sexto ponto de controle do arquivo cp_upper.inp.

Depois faça um teste retirando do extradorso o quinto e sexto pontos de controle.

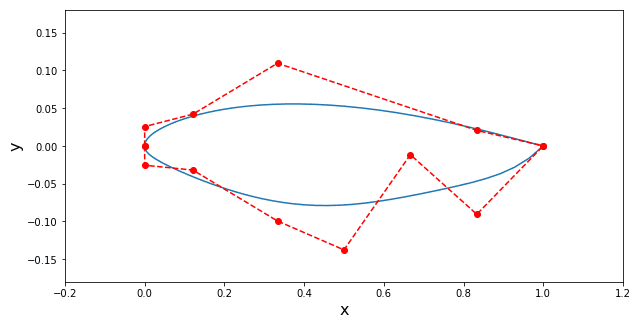
Note que ao retira dois pontos de controle a ordem do polinômio que representa o extradorso diminuiu em relação ao intradorso. Outro aspecto que você deve ter notado é que não existem restrições impostas aos pontos de controle. Assim, se você colocar a coordenada Y de um ponto de controle em uma posição muito distante em relação aos demais provavelmente gerará um perfil disforme. As restrições serão abordadas na seção de otimização deste artigo.

Outra aplicação consiste na modificação de regiões específicas de um determinado aerofólio. O conjunto de imagens abaixo mostra a alteração do bordo de ataque do perfil através das sucessivas modificações nos pontos de controle. Inicialmente têm-se os pontos de controle que restituem o bordo de ataque da geometria e posteriormente são realizadas modificações em alguns destes pontos de controle.

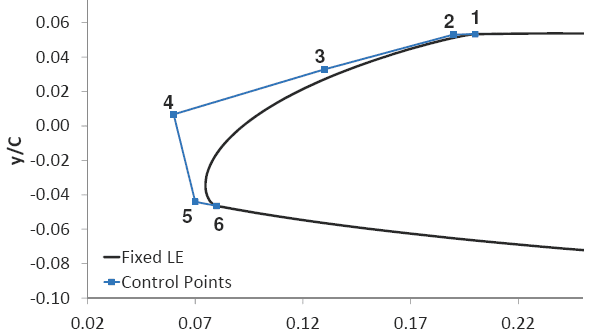
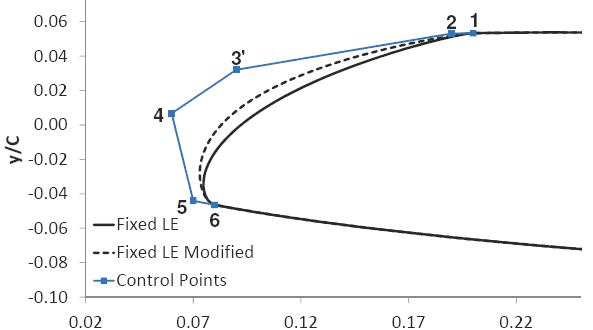
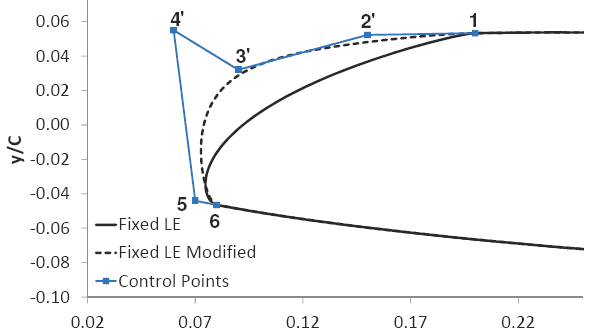
Até esse momento não foi comentado, mas para obtermos os pontos de controle que reproduzem uma dada geometria de interesse (curva de arqueamento e de espessura relativa) é necessário realizarmos inicialmente um “processo inverso”. Depois podemos modificar os pontos de controle para alterar a geometria. A figura abaixo mostra novamente a aplicação deste mesmo conceito de “processo inverso”, só que agora não aplicado nas curvas de espessura e de arqueamento, mas sim na própria geometria do perfil de interesse.

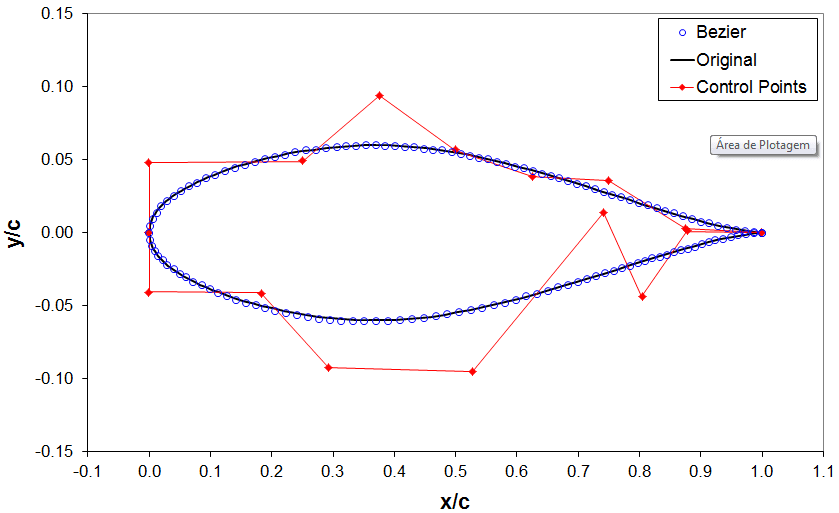
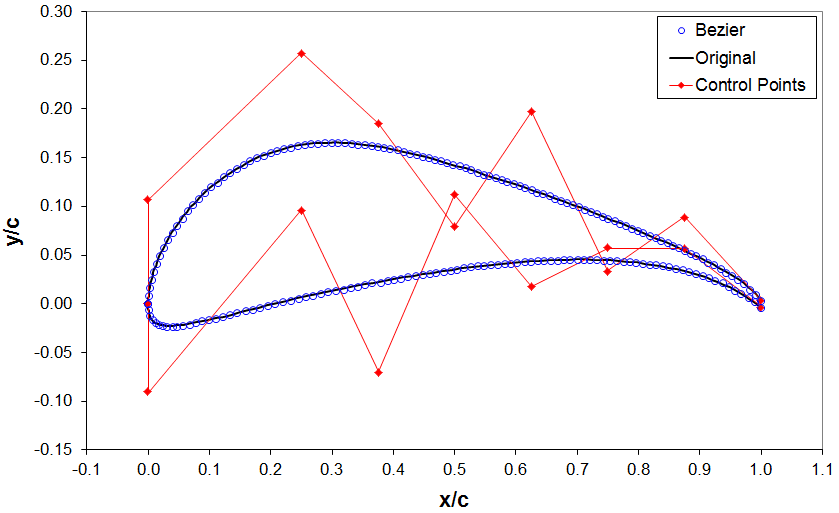
Na verdade temos que escrever as equações de Bézier na forma inversa para obter os pontos de controle iniciais e, posteriormente, realizar um processo de otimização no qual buscamos minimizar a diferença entre a geometria corrente e a geometria ‘target’.

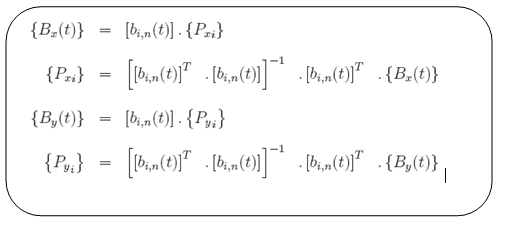
Esse “processo inverso” será abordado em um dos cursos de projeto e otimização com todos os detalhes das manipulações algébricas necessárias. Neste mesmo curso os detalhes sobre as demais parametrizações também serão abordados.

Até o presente momento abordamos os coeficientes aerodinâmicos de um perfil, os esforços empregados no desenvolvimento de perfis aerodinâmicos e apresentamos, ainda que rapidamente, um conceito de parametrização geométrica. O próximo passo consiste em abordar as análises numéricas para obtenção dos coeficientes aerodinâmicos. No entanto, antes de entrarmos nos aspectos operacionais das simulações numéricas é importante que conceitos básicos de aerodinâmica sejam apresentados, até porque estes conceitos irão contribuir com o entendimento dos critérios aerodinâmicos demandados para o projeto de um determinado perfil. Conforme mencionado anteriormente iremos montar a visão sobre projeto e otimização passo a passo. Então até o próximo artigo!

CLIQUE NOS LINK ABAIXO PARA BAIXAR: 

CÓDIGO DE GERAÇÃO DE PERFIL BÉZIER

EXEMPLO DE CURVAS DE BÉZIER – PLANILHA EXCEL

O que acha de conhecer mais lendo um artigo?

O Portal tem diversos conteúdos para te ajudar a se qualificar para o mercado de trabalho. Dê uma lida nesse artigo, depois conta pra gente o que achou!

Quer conhecer mais sobre o Portal Engenharia Aeronáutica?

▶ INSCREVA-SE no nosso canal do Youtube! Vem com a gente e embarque no mundo da aviação!

https://www.youtube.com/c/EngenhariaAeronáutica?sub_confirmation=1

Siga a gente nas redes sociais!

▶ Facebook: https://www.facebook.com/engenhariaaeronauticabr/

▶ Instagram: @engenhariaaeronautica (https://www.instagram.com/engenhariaaeronautica/)