Conceitos de Aerodinâmica

Pessoal, neste artigo vamos abordar alguns conceitos de aerodinâmica, pois precisamos ter conhecimento da física para podermos interpretar os resultados que são obtidos durante as análises de otimização. Então vamos lá!

Conceitos de Aerodinâmica

Este tópico não pretende ser uma completa e extensiva aula sobre aerodinâmica, mas busca enumerar alguns dos principais conceitos que você precisará conhecer. Caso tenha alguma dúvida sobre a teoria apresentada sugiro que busque o curso de Aerodinâmica Aplicada do Rodrigo Sorbilli.

Antes de começar a apresentar alguns dos conceitos de aerodinâmica vale a pena comentar que dado um fenômeno físico escrevemos equações matemáticas, ou equações governantes, para representar este fenômeno de interesse. Estas equações matemáticas podem ser resolvidas numericamente através do emprego de diferentes métodos numéricos (em alguns casos muito particulares conseguimos uma solução analítica para a equação governante). No entanto, quando o custo computacional para a obtenção da solução é extremamente alto, ou não se tem o recurso computacional para executar tais simulações, medidas como simplificações de termos das equações governantes podem ocorrer. Ou seja, abre-se mão de captura de alguns dos fenômenos físicos em prol da viabilidade de se obter alguma informação, também importante, através da simulação numérica simplificada. A imagem abaixo mostra que o custo computacional cresce à medida que adotamos métodos numéricos que representam cada vez melhor os fenômenos físicos.

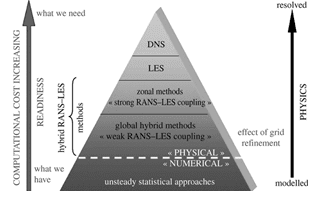
Visualmente as duas figuras abaixo ilustram bem o que representa este processo de simplificação. Na figura a esquerda tem-se o campo médio do escoamento. Ou seja, estamos capturando as propriedades médias do escoamento quando o fluido escoa neste degrau. Já na figura da direita conseguimos ver uma melhor definição das estruturas que estão presente no escoamento. Para capturar estas estruturas com mais detalhes paga-se um considerável preço adicional em termos de custo computacional.

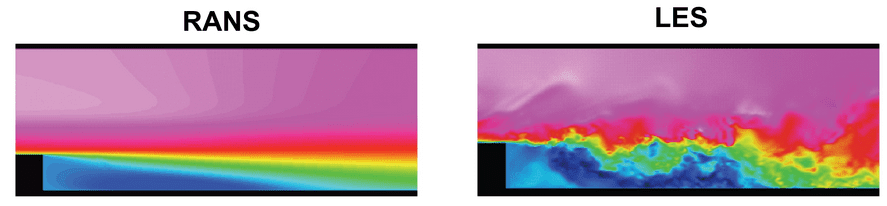
Os comentários acima mencionados serão tratados com todos os detalhes pertinentes no curso de CFD que estará disponível no portal.

O que será apresentado a seguir são equacionamentos simplificados, mas que possibilitam o ganho de “insights” sobre as características aerodinâmicas das análises em questão. Mais a frente, quando falarmos sobre as simulações, não entraremos nos detalhes da formulação numérica, pois estaremos usando os códigos como uma caixa preta no processo de otimização. No entanto, devemos conhecer a física para que possamos escolher o código com a formulação adequada para o estudo de interesse.

Equação de Bernoulli – Relaciona a pressão e velocidade entre dois pontos quaisquer de uma linha de corrente. Esta equação é obtida a partir das equações de Navier-Stokes, mas com as seguintes simplificações: fluido não viscoso, escoamento estacionário e incompressível. Se o escoamento for não rotacional então a equação de Benoulli tem validade entre quaisquer dois pontos do escoamento.

Fluido não Viscoso: a viscosidade é considerada nula e o escoamento não adere à parede.

Escoamento Estacionário: as propriedades do escoamento variam em função apenas das coordenadas.

Escoamento Incompressível: não existe efeito de variação de densidade no campo do escoamento.

A equação de Bernoulli é dada pela seguinte expressão:

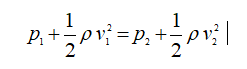
Onde, p é a pressão estática, v é a velocidade e ρ é a densidade. Este princípio permite explicar o motivo pelo qual quando a velocidade aumenta no extradorso do perfil a pressão é reduzida e como consequência tem-se uma força resultante que gera a sustentação.

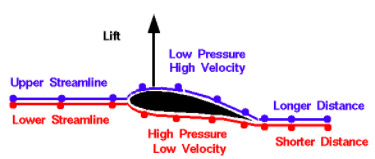
Uma aeronave em voo é um corpo que se movimenta com determinada velocidade em relação a um meio que por simplicidade vamos supor que esteja parado. Podemos mudar o sistema de referência e considerar que a aeronave está parada e o meio, neste caso o ar, se movimenta com a velocidade da aeronave.

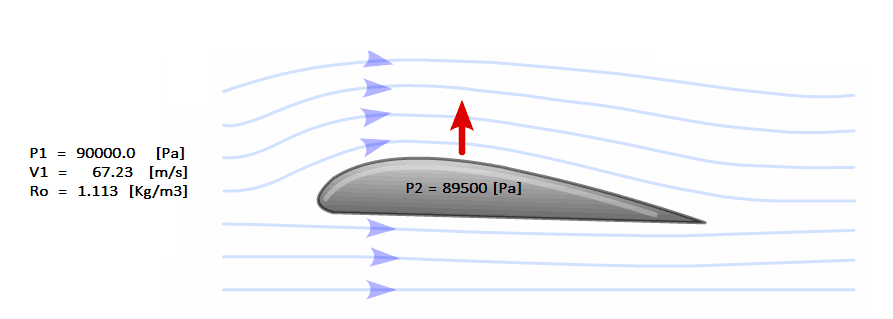
Quiz: Então, supondo que o ar longe do perfil tenha as propriedades definidas na figura abaixo (P1, V1 e Ro) qual a velocidade no ponto definido pela seta vermelha se a pressão neste ponto for de 89500 [Pa]? Esse é um exemplo da aplicação da equação de Bernoulli. Não se esqueçam das hipóteses levantadas para a validade da formulação.

A utilização da equação de Bernoulli não possibilita a obtenção da distribuição de pressão em corpos aerodinâmicos para uma determinada condição de voo. Repare que precisamos conhecer alguma propriedade sobre o corpo para definir a outra, seja esta a velocidade ou a pressão!

Vamos abordar agora a equação da conservação da massa, pois podemos utilizar este princípio em conjunto com a equação de Bernoulli para realizar o cálculo da velocidade em diferentes pontos de interesse. A equação da conservação da massa quando descrita para um escoamento estacionário e incompressível pode ser expressa pela equação abaixo.

Área x Velocidade=Const

Na figura abaixo, temos uma superfície de área A e vamos considerar uma fração desta área dada por dA. Nesta região definida por dA temos a definição de um vetor de velocidade normal a esta área, dado do V. Supondo que esta região dA esteja se deslocando juntamente com o vetor de velocidade V, então, após um intervalo de tempo t teremos andado uma distância L, dada por (V.t) , e teremos um volume dado por (dA.V.t). Lembrando que massa = volume x densidade, então temos que massa = (dA.V.t.ρ), passando o termo t para o outro lado da igualdade teremos m/t = (dA.V.ρ). Ou seja, o fluxo de massa [Kg/s] é igual à área x velocidade x densidade. Hipótese de escoamento estacionário.

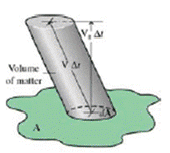
O escoamento sendo estacionário e incompressível a equação da continuidade pode ser representada pela expressão abaixo. A densidade é igual entre dois pontos distintos e pode ser desconsiderada da expressão.

conceitos de aerodinâmica

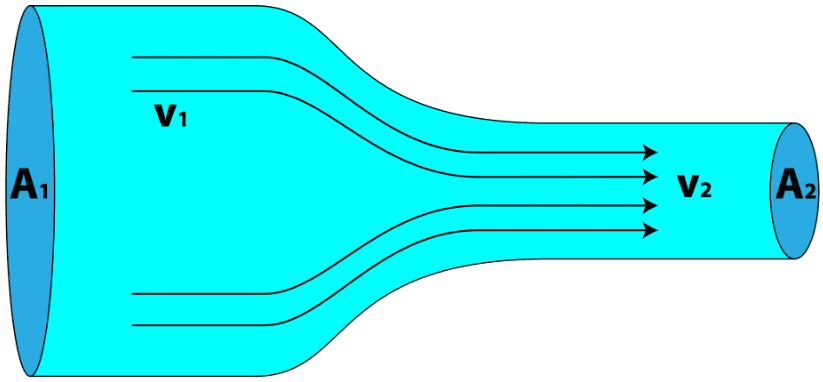
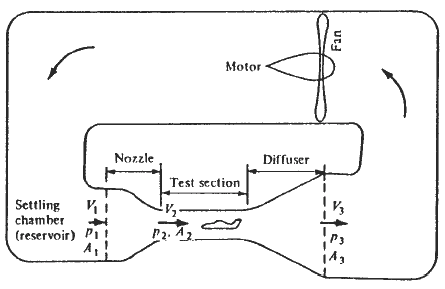
Assim, sabendo as razões de áreas, como na figura acima, podemos definir a relação entre velocidades em dois pontos. Esta informação é importante, pois se trata de uma das variáveis da equação de Bernoulli. Para ilustrar o conceito podemos usar como exemplo diferentes seções de um túnel de vento subsônico. Dada à pressão e velocidade em um determinado ponto (Ponto 1), se soubermos a razão entre as áreas com respeito a outras seções do túnel de vento (Ponto 2 e Ponto 3) conseguimos definir a velocidade e pressão nestas outras duas seções.

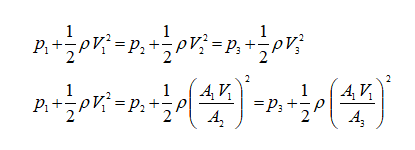
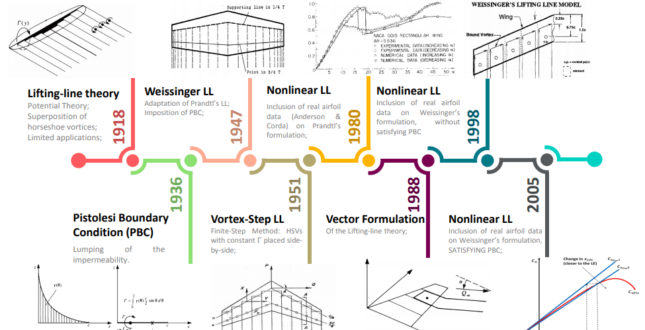
Escoamento Potencial – Para um escoamento irrotacional (rotacional da velocidade é nulo) existe uma função escalar φ (potencial de velocidade), tal que, a velocidade é dada pelo gradiente de φ. Se o escoamento for incompressível, então, o divergente da velocidade é nulo e através da substituição das igualdades chegamos à equação de Laplace. Bem, você precisa saber que os códigos baseados em escoamento potencial estão resolvendo a equação de Laplace!

A solução desta equação, com a aplicação das condições de contorno pertinentes (condição de Kutta e velocidade transversal à parede igual a zero), provê o campo de pressão em geometrias de interesse aeronáutico como um aerofólio ou uma asa (linha sustentadora, métodos de Weissinger, vortex lattice e método dos painéis). A grande vantagem destas abordagens reside na rápida obtenção da distribuição de pressão e velocidade para uma dada configuração de interesse. Já a desvantagem consiste no fato de que algumas destas formulações não serem capazes de capturarem os efeitos associados a descolamentos do escoamento (efeitos viscosos) e os efeitos de compressibilidade do escoamento.

conceitos de aerodinâmica

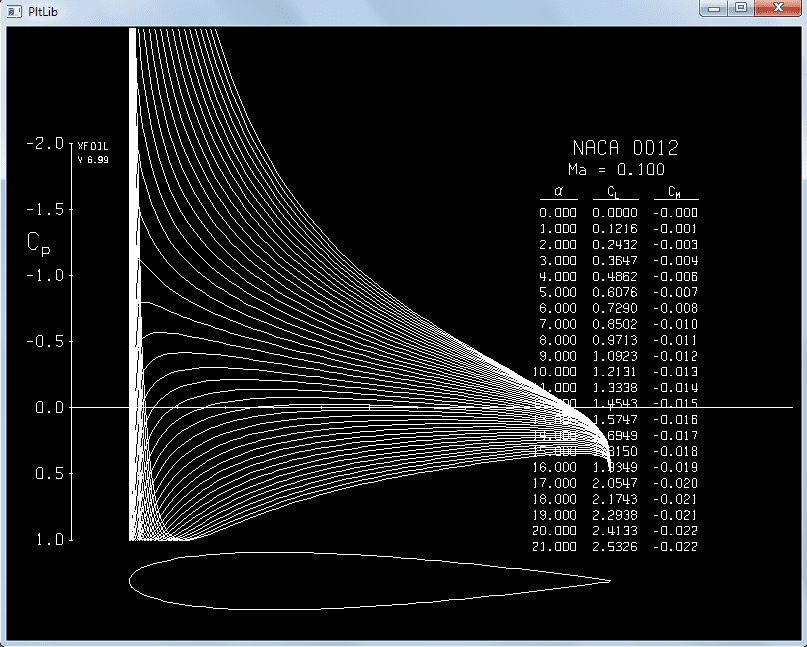
O XFOIL é um ‘solver’ aberto que usa o método de painéis para obtenção da distribuição de pressão para um dado perfil aerodinâmico de interesse e que tenha sido dado como entrada. Este código também possui uma sub-rotina de camada limite para capturar os efeitos viscosos (a camada limite é abordada no próximo artigo). Vamos utilizar este software apenas considerando o método de painéis para dar uma ideia da velocidade para obtenção do resultado e os efeitos nos resultados pelo fato de não capturarmos os efeitos viscosos do escoamento. Siga os passos indicados a seguir.

Faça o download do XFOIL no site https://web.mit.edu/drela/Public/web/xfoil/
Use o programa ZIP para ‘descompactar’ o arquivo e execute o xfoil.exe com um ‘double click’ no arquivo *.exe.
Ao abrir a janela digite a sequência de comandos:

naca0012
oper
mach
1
aseq
0
21
1

Teoricamente a sequencia de comandos acima deveria executar a simulação. Caso não seja possível veja na tela do aplicativo a descrição de cada comando. Se tudo der certo após esta sequência de comandos a distribuição de pressão aparecerá quase que instantaneamente na tela.

A figura abaixo mostra o resultado obtido com o XFOIL e o resultado experimental para o número de Reynolds de 3, 6 e 9 milhões, imagem à esquerda. Note que o resultado experimental apresenta o ‘stall’ aerodinâmico para o AoA = 16°, enquanto que a simulação numérica não captura o fenômeno do ‘stall’. Essa é uma limitação da formulação potencial. Se você continuar aumentando o ângulo de ataque do perfil à simulação continuará a gerar sustentação. Isso não ocorre na vida real!

conceitos de aerodinâmica

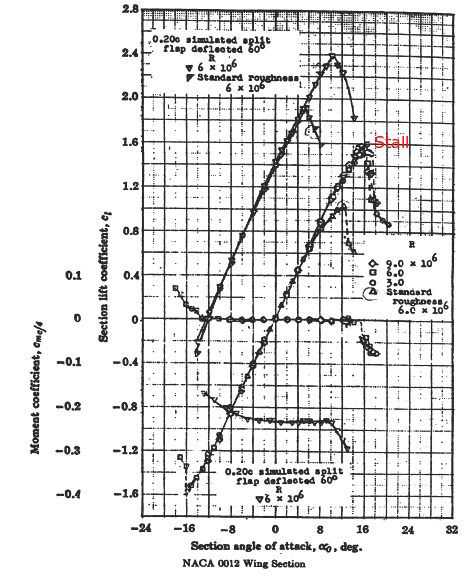
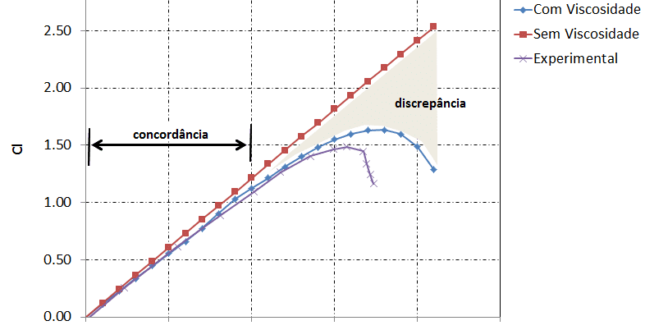
A figura abaixo mostra uma comparação entre a simulação do XFOIL sem a viscosidade, solução considerando apenas a solução potencial, e a simulação considerando o modelo de camada limite do XFOIL. Nesta mesma figura também podemos ver os resultados experimentais para número de Reynolds de três milhões. O resultado do XFOIL, com o modelo de camada limite, tem uma boa correlação com o resultado experimental para faixa de ângulo de ataque até 15°. O resultado numérico prevê um ‘stall’ em um ângulo de ataque um pouco maior e com um valor maior de Cl.

Para o resultado potencial do XFOIL a discrepância é maior. No entanto, para ângulos de ataque na faixa situada entre [0°, 10°] existe uma correlação razoável para o coeficiente de sustentação, Cl. De uma maneira geral os fenômenos viscosos “não se manifestam[1]” na região linear. Note que a afirmação se baseia na premissa de que estamos no regime subsônico e que não temos regiões com descolamento massivo nesta faixa de ângulos de ataque. Aqui a formulação potencial apresenta resultados que podem ser utilizados para algumas das análises aerodinâmicas. Hipótese: não existência de descolamentos do escoamento nesta região linear.

[1] Efeitos não lineares ocorrem nos ângulos de ataque maiores e a partir do qual se começa a observar efeitos associados ao descolamento do escoamento. Quando a Camada Limite for abordada neste artigo, uma explicação melhor será dada para o termo ‘efeitos não lineares’.

conceitos de aerodinâmica

Quiz: Se você tiver interesse em otimizar um perfil para aumentar o Cl máximo do mesmo você usaria a formulação do métodos de painéis?

Parece que a captura dos efeitos viscosos pela simulação numérica é algo importante. Então, será que sempre precisaremos considerar a adoção de um ‘solver’ que contemple os termos viscosos? Na verdade não necessariamente, enquanto a análise de interesse estiver na região linear e dependendo do que se queira observar do comportamento aerodinâmico, uma formulação potencial pode ser adequada. Um exemplo disso é o uso de métodos potenciais para o cálculo do arrasto induzido da aeronave.

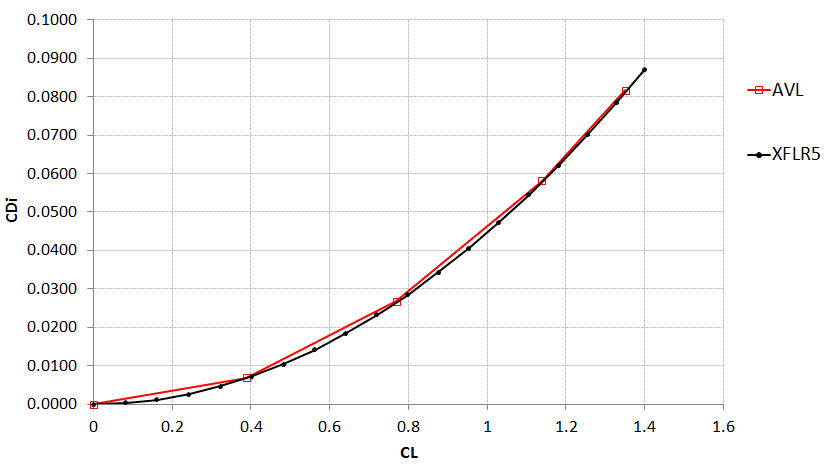
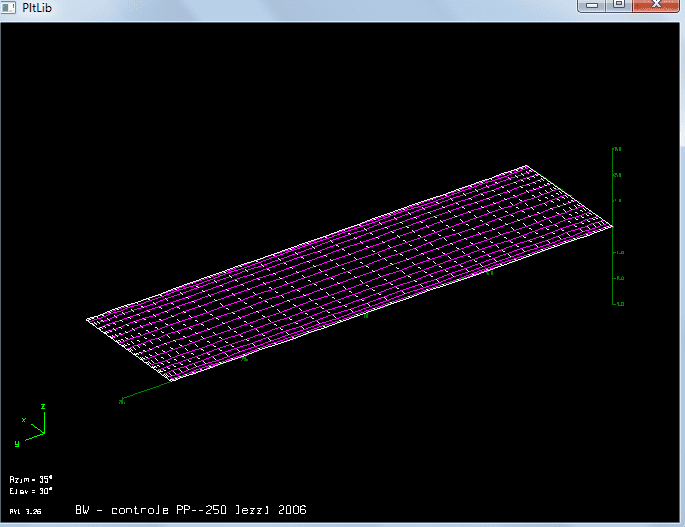
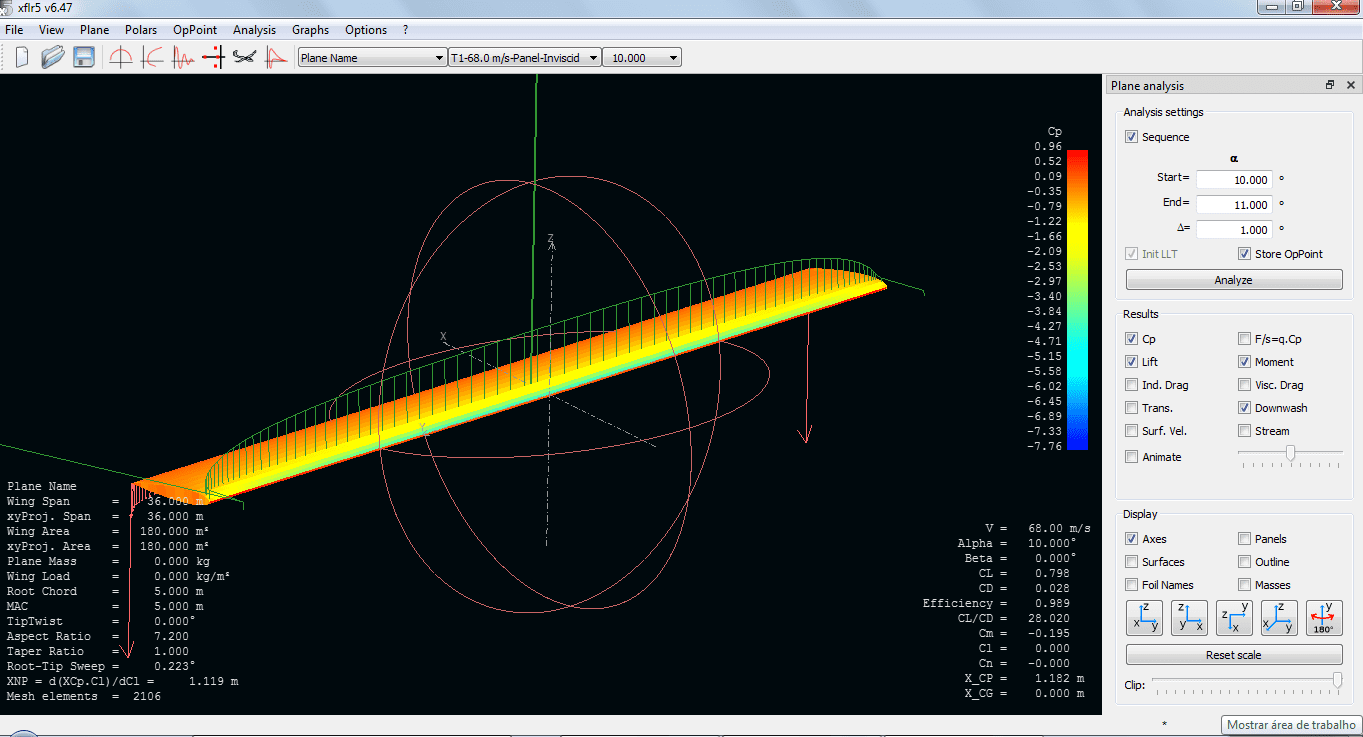
A imagem abaixo mostra o arrasto induzido em função do coeficiente de sustentação para uma asa reta e construída a partir do perfil NACA0012. Foram considerados dois perfis um na raíz e outro na ponta da asa. Estes resultados foram obtidos pelos códigos AVL e XFLR5. Notem que existe uma boa aderência entre as duas ferramentas para a previsão do arrasto induzido deste exemplo em função do coeficiente de sustentação.

Os links para o download destes dois aplicativos estão descritos abaixo. Conforme mencionado anteriormente os códigos serão tratados como “caixas pretas”. No entanto, precisamos conhecer qual a formulação das equações governantes e como operá-los, pois os mesmos serão integrados em ambientes de otimização. Quando abordamos o tema sobre os códigos voltarei a comentar sobre o AVL e o XFLR5.

AVL	http://web.mit.edu/drela/Public/web/avl/
XFLR5	http://www.xflr5.tech/xflr5.htm

conceitos de aerodinâmica

Um comentário importante a ser feito aqui é que o arrasto induzido é uma das parcelas do arrasto total, as demais são o arrasto de fricção, o de pressão e o arrasto de onda no caso de uma condição de voo transônica. A decomposição de arrasto será apresentada no próximo artigo, mas o importante, neste momento, é saber que o arrasto total contempla a contribuição de várias parcelas.

conceitos de aerodinâmica

O que acha de conhecer mais lendo um artigo?

O Portal tem diversos conteúdos para te ajudar a se qualificar para o mercado de trabalho. Dê uma lida nesse artigo, depois conta pra gente o que achou!