Hands-On AVL

Neste artigo iremos abordar qual a melhor ponta de asa para ser instalada em uma asa retangular sem afilamento e sem torção geométrica. Neste estudo de otimização iremos considerar dois cenários. No primeiro cenário buscaremos a configuração da ponta de asa que minimiza o arrasto induzido desta asa retangular de referência. Já no segundo cenário consideraremos a configuração que produz ao menor momento na raiz da asa (BMX). Ambos os estudos serão realizados considerando o aplicativo AVL (site: http://web.mit.edu/drela/Public/web/avl/).

Caso o leitor encontre alguma dificuldade em algum ponto do texto a seguir, sugiro que dê uma olhada no artigo: “Hands-On” Otimização com o XFOIL. Neste artigo eu também explico o processo de setup de um estudo de otimização. Assim, pode ser que você encontre alguma explicação para algum ponto que não tenha ficado claro neste texto, embora tenha tomado o cuidado para deixar o mais elucidativo quanto possível.

Estudo de Caso N°01 – Minimizar o Arrasto Induzido de uma Asa Retangular

Neste exemplo queremos minimizar o arrasto induzido de uma asa reta sem afilamento e sem torção através da instalação de uma ponta de asa. A otimização será realizada usando o algoritmo SGA – Single Genetic Algorithm que você já obteve no site do portal (são os seguintes arquivos: GA_Class.py, GA_setup.py e Sobol.py).

O código utilizado neste estudo é o AVL e a asa tem uma corda constante de 2.0 [m] com uma envergadura de 24 [m] e área de referência de 48.0 [m²]. O ‘statement’ da otimização é dado abaixo, sendo que, as duas principais variáveis de projeto são os ângulos formados entre o plano da asa e o plano vertical de cada segmento desta ponta que também pode ser chamada de winglet. Os segmentos da winglet possuem um comprimento fixo de 2.0 [m] e estes ângulos podem variar de 0° a 90°.

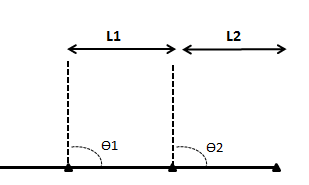
Com a definição destes limites para os ângulos dos segmentos da winglets, algumas das formas geométricas que podem ser obtidas são ilustradas abaixo. O otimizador irá definir qual a melhor configuração para cada um dos cenários que serão estudados (na verdade a melhor forma para minimizar a funções objetiva definida).

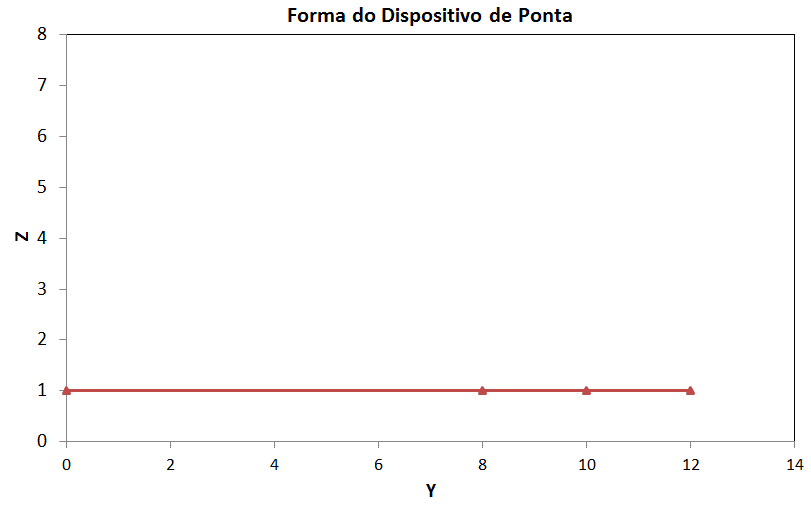
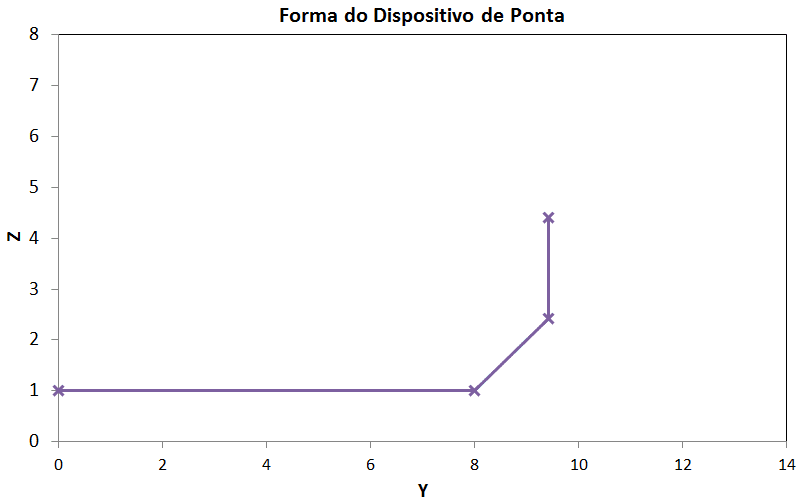
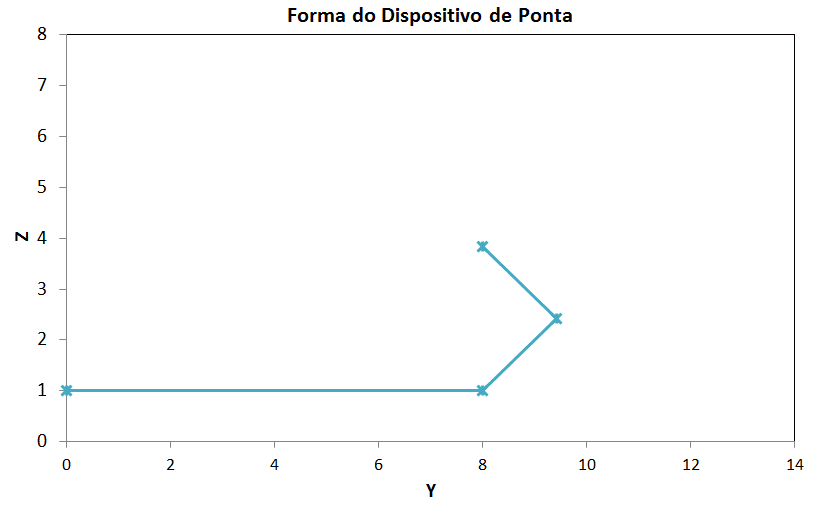
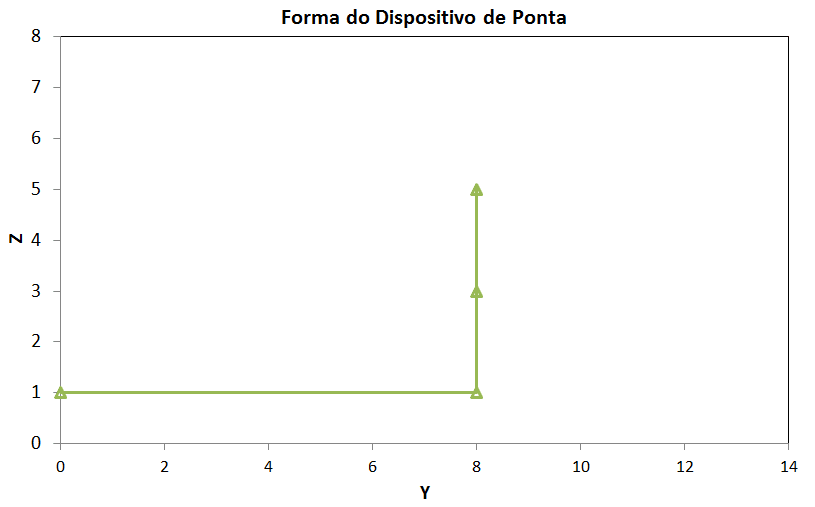
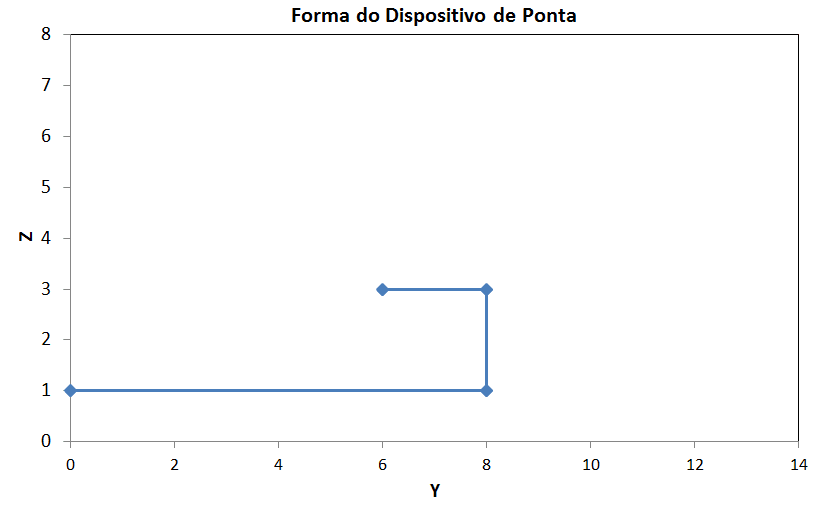
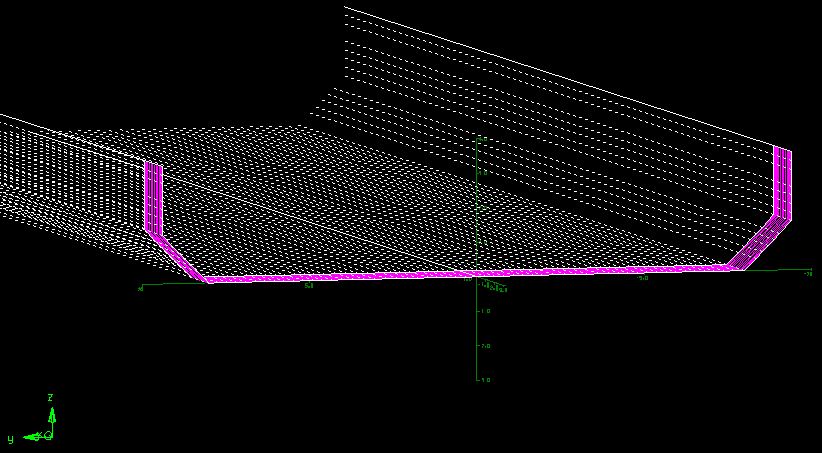
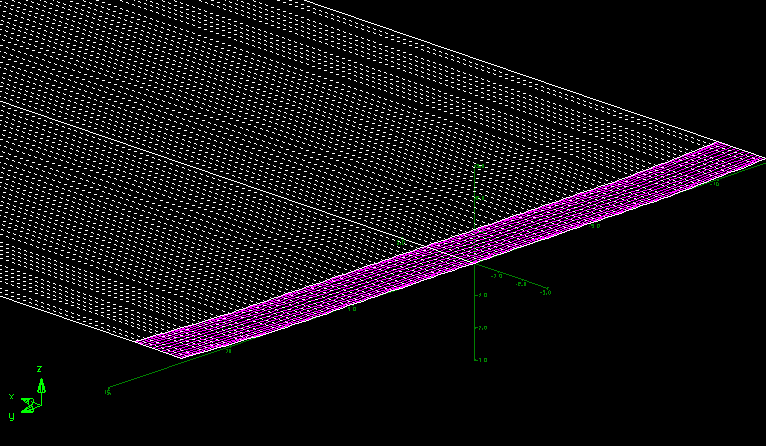
Exemplo do modelo gerado para o AVL em função dos valores dos ângulos dos segmentos das winglets.

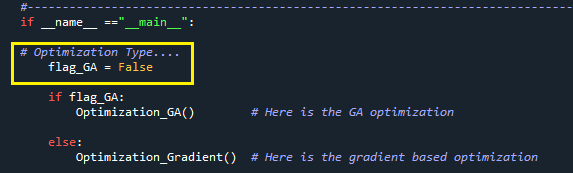
O programa AVL_Opt_Induce_Drag.py tem uma função “__main__” que é o core do programa. Nesta parte do programa você precisa definir qual método de otimização você gostaria de utilizar. O default do arquivo obtido no site está para o método de otimização usando algoritmos genéticos (flag_GA = True).

Lembre-se de colocar os arquivos GA_Class.py, GA_setup.py, Sobol.py, naca0012.dat e ga_setup.inp no diretório onde realizará as simulações. Os três primeiros arquivos contemplam a implementação do SGA, Single Genetic Algorithm. O arquivo naca0012.dat é utilizado para que o AVL obtenha as informações de camber e de espessura do perfil. Já o arquivo ga_setup.inp contem o setup do algoritmo genético conforme pode ser visto na imagem abaixo.

As definições do input deste arquivo já foram descritas no artigo anterior quando otimizamos um perfil, mas estou apresentando novamente as definições. Sugiro fazer a primeira simulação sem alterar o setup do arquivo que foi obtido no site, assim você pode verificar se está tudo operacional na sua máquina. Depois se sinta a vontade para fazer as alterações do seu interesse. Abaixo a descrição das variáveis.

Generation – número de gerações na buscar pela melhor solução.

Population – número soluções (conhecidas como indivíduos) com que o otimizador trabalha de maneira simultânea.

Pmut – probabilidade de mutação de uma dada variável de projeto.

Pcross – probabilidade da realização do “cross-over” entre dois indivíduos que foram pareados.

Mating_Pool – Número de indivíduos que irão participar do “mating-pool”.

Type – o algoritmo pode trabalha com a representação binária ou real das variáveis de projeto.

BLX-alpha – parâmetro para a codificação real e que indica o coeficiente da distribuição de probabilidade para uma dada variável de projeto.

Var_size – consiste nu tamanho da string binária para representar uma determinada variável.

Variables – número de variáveis de projeto.

Var_Lower – limite inferior para as variáveis de projeto.

Var_Upper – limite superior para as variáveis de projeto.

Note que os valores dos limites das deflexões de cada segmento da winglets podem ser alterados na definição das variáveis Var_Lower e Var_Upper.

A figura abaixo mostra a chamada do método que realiza a otimização com a implementação do SGA. Para executar esta otimização o método Run_AVL é passado para o método Opt_SGA do objeto ga.

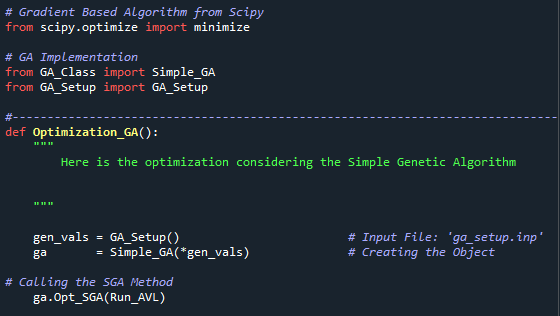
Você também pode usar algum outro método baseado em gradiente. Neste caso é necessário fornecer uma condição inicial para o algoritmo de otimização conforme mostrado na imagem abaixo. (Não se esqueça de fazer a seguinte modificação flag_GA = False na função “__main__”).

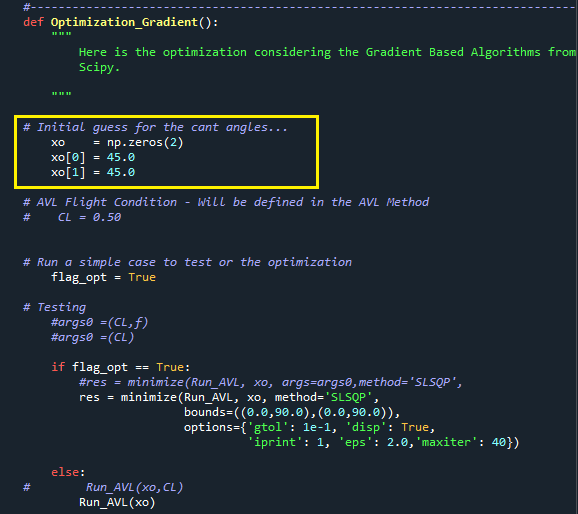
Repare que o método Optimization_Gradient (imagem acima) tem a variável flag_opt. Esta variável possibilita que você rode uma simulação do AVL sem executar a otimização, para tanto é necessário definir flag_opt = False. A simulação será feita para os valores que você definiu para as variáveis xo[0] e xo[1], conforme pode ser visto na imagem acima. Não se esqueça de voltar a variável flag_opt para True para possibilitar o processo de otimização com o método de gradiente.

O método SLSQP foi definido para o processo de otimização baseado em gradientes. Para maiores detalhes quando for alterar o algoritmo de otimização busque a página abaixo. Alguns métodos demandam inputs adicionais, então, é importante saber estes detalhes caso contrário o código poderá dar um “crash”.

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

AVL

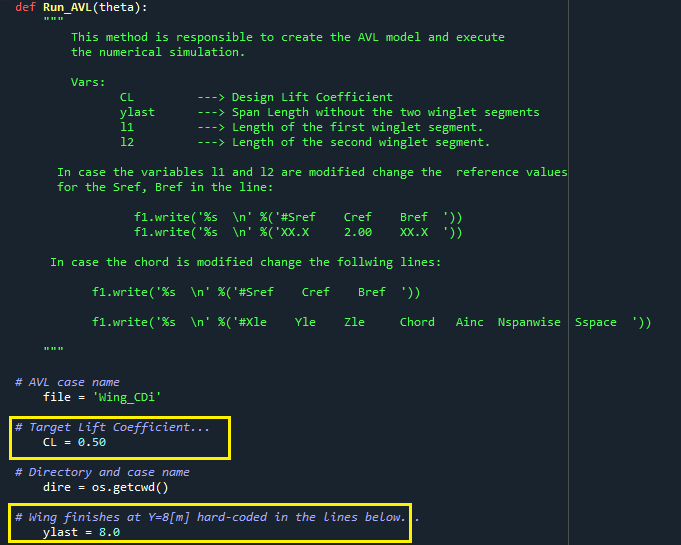
No método Run_AVL é onde o arquivo de entrada do AVL é gerado. As variáveis para os comprimentos das winglets, o valor do coeficiente de sustentação, CL, e a corda da asa são informações “hard-coded”. Se você quiser modificar estes dados no começo do método os detalhes de como proceder são descritos nas imagens abaixo. Mas lembre-se de alterar também os valores de referência para a envergadura e área de referência da asa caso faça modificações.

Na imagem abaixo está à definição do CL da simulação e o tamanho do span da asa de referência (asa sem os dois segmentos da winglet). Os valores de L1 e L2 também podem ser alterados conforme indicado na figura. Estes parâmetros são as variáveis l1 e l2.

AVL

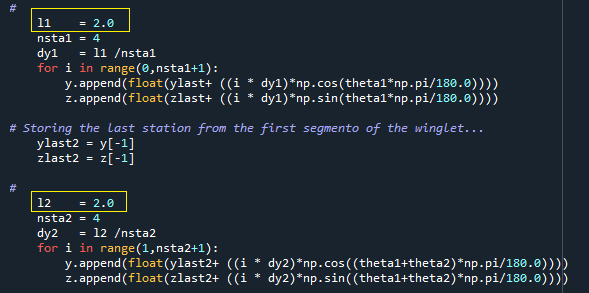
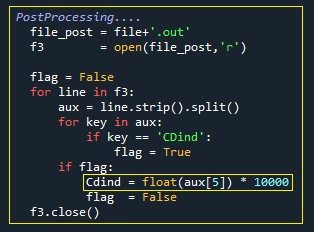
No método Run_AVL também temos o pós-processamento da simulação. No arquivo de output do AVL o código busca a variável CDind, que é o arrasto induzido, e multiplica este valor por 10000 para transformar o resultado em drag count. Logo em seguida o valor do momento fletor na raíz, bmx, é obtido como um output do método Post_Bending.

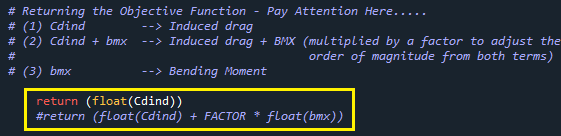
A função objetiva é aquela que o método retorna para o otimizador, como pode ser visto na imagem abaixo. Note que o pós-processamento do método está adquirindo apenas o valor do arrasto induzido e do momento fletor (método Post_Bending). Você pode altera o código para obter outros coeficientes aerodinâmicos e compor a sua função objetiva pela soma ponderada dos mesmos. Repare que você vai precisar definir alguns fatores para que os diferentes coeficientes aerodinâmicos tenham a mesma ordem de grandeza. Caso contrário se um dos termo da função objetiva tiver um valor muito maior do que os demais, o otimizador vai procurar a solução que maximize ou minimize este termo e passa a “ignorar” os demais. Abaixo o exemplo onde retorno apenas o CDind para o otimizador. Note como seria o caso onde faço a composição do Cdind e do bmx.

AVL

Os seguintes arquivos são gerados durante a simulação:

Wing_CDi.avl – Modelo AVL

Wing_CDi.run – Comandos para rodar em batch

Wing_CDi.out – Arrasto Induzido da configuração analisada.

Wing_CDi_bending.out – Momento fletor do modelo.

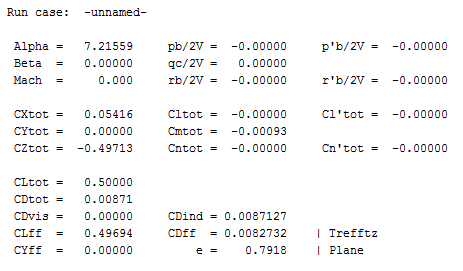
O arquivo de Wing_CDi.out tem o formato descrito pela imagem abaixo. Caso queiram minimizar algum outro coeficiente aerodinâmico, então, deve-se mudar o key == ‘CDind’ para o nome do coeficiente de interesse. Não esquecer que neste exemplo apenas o ângulo das winglets estão sendo alterados!

AVL

O arquivo de Wing_CDi_bending.out tem o formato descrito pela imagem abaixo.

AVL

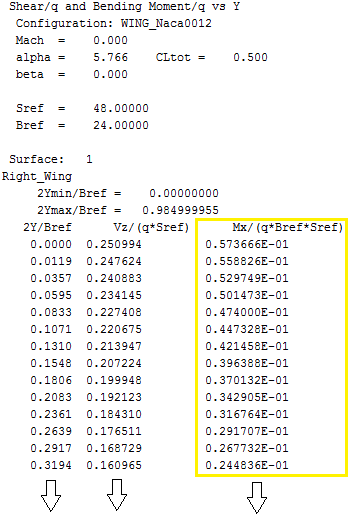
O método Post_Bending faz o somatório do Mx ao longo da envergadura da asa e retorna para o método Run_AVL.

ATENÇÃO: Um detalhe que não pode passar despercebido consiste no fato de que os GA’s são algoritmos que buscam obter o valor máximo de uma função. Assim, se você quiser minimizar a função objetiva, vamos supor o CDi, então, deve passar para o método do GA o valor Obj=1/CDi. Ou seja, algoritmo vai maximizar Obj buscando valore mínimos de CDi que é o que você deseja. Logo, no final do método Run_AVL mude o código para:

return 1/Cdind

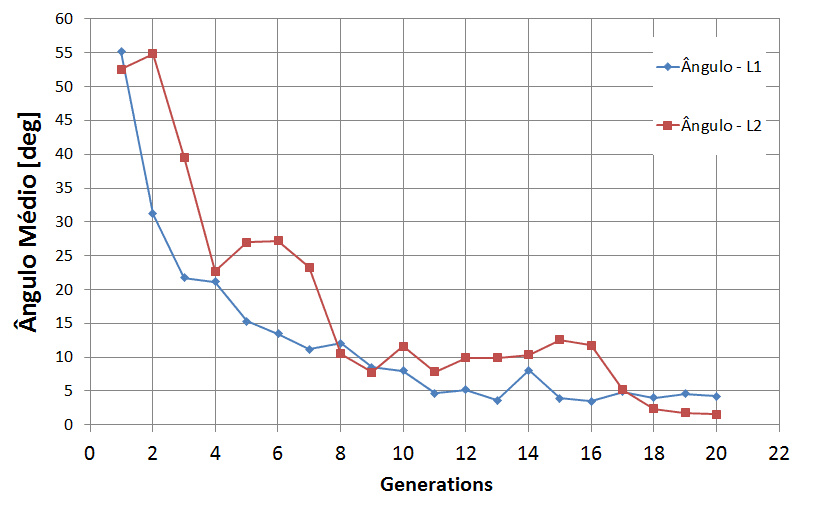
O resultado obtido para a otimização do arrasto induzido levou a uma winglet com os seguintes ângulos ótimos ϴ₁ = 1.64° e ϴ₂ = 0.72°. Notem que provavelmente estes valores iriam para zero caso a otimização tivesse mais gerações e um número maior de indivíduos.

AVL

A imagem abaixo mostra o valor médio dos ângulos ϴ₁ e ϴ₂ ao longo das sucessivas gerações do processo de otimização. Notem que o valor é maior do que o mínimo, pois se trata da média de cada geração. Além do mais como temos o operador mutação, que pode gerar valor grande para os ângulos, acabamos com um resultado acima do mínimo, mas isso é normal.

AVL

Estudo de Caso N°02 – Minimizar o Momento fletor de uma Ponta de Asa

Neste exemplo queremos minimizar o momento fletor da ponta de asa inserida em uma asa retangular sem afilamento e sem torção. A otimização também foi realizada usando o algoritmo SGA.

A figura abaixo apresenta o valor do ângulo médio ao longo de cada uma das gerações do processo de otimização. Vemos que o valor médio converge para algo próximo de 90° para ambos os segmentos, L1 e L2. Não atinge exatamente o valor de 90° pois conforme explicado anteriormente o algoritmo SGA tem a operação de mutação que leva ao aparecimento de soluções alternativas (qualquer dúvida veja a definição dos operadores dos algoritmos genéticos no artigo Algoritmos de Otimização).

AVL

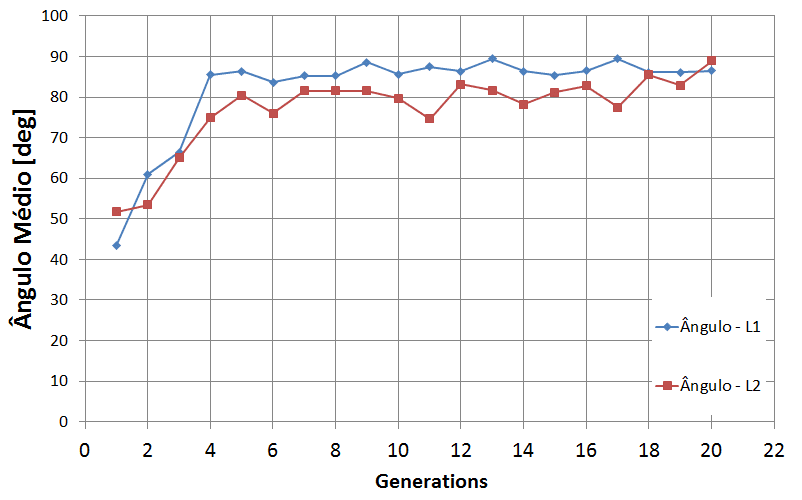
A imagem abaixo mostra os valores ótimos para os ângulos dos dois segmentos das winglets ϴ₁ = 89.92° e ϴ₂ = 89.89°.

AVL

Exercício

Façam uma otimização para o bmx e usando o método de gradiente. Coloquem o seguinte range para o ângulo [-90.0, 90.0] e primeiro iniciem com os valores ϴ₁ = -45.00° e ϴ₂ = -45.00°. O resultado convergiu para que valor final?

Agora faça novamente a otimização, mas coloque inicie com os seguintes ângulos ϴ₁ = 45.00° e ϴ₂ = 45.00°. O resultado convergiu para que valor final?

O arrasto induzido é igual nos dois casos? Por que?

Arquivos: Projeto_e_Otimização_Hands-On_AVL

Input e Programas Adicionais:

AVL_Opt_Induced_Drag.py

GA_Class.py

GA_Setup.py

Sobol.py

naca0012.dat

ga_setup.inp

O que acha de conhecer mais lendo um artigo?

O Portal tem diversos conteúdos para te ajudar a se qualificar para o mercado de trabalho. Dê uma lida nesse artigo, depois conta pra gente o que achou!