Hands-On Otimização com o Xfoil

Bem, neste artigo iremos consolidar tudo o que vimos até então. Na verdade neste momento iremos de fato colocar a “mão na massa” com o Xfoil. Então, vamos lá!

Estudo de Caso N°01 – Otimização Aerofólio Simétrico

O código descrito a seguir foi desenvolvido com objetivo de executar otimizações aerodinâmica considerando um perfil simétrico. As curvas de Bézier são adotadas para fazer a parametrização geométrica do perfil e o código XFOIL é utilizado para executar a simulação. Antes de mexer no setup do código, que contempla o algoritmo de otimização, “rode” o mesmo sem alterar os arquivos da página do portal.

Verifique se o código está “rodando” e se não está faltando algum arquivo ou pacote do Python. A princípio os arquivos disponibilizados com os respectivos diretórios estão preparados para “rodar” sem problemas, mas você precisa colocar o executável do XFOIL no seu diretório de trabalho. Um vídeo bem simples está disponível no portal parar mostrar o código “rodando”, é esperado que você obtivesse algo semelhante ao do vídeo.

Se tudo ocorreu bem, vamos agora para as explicações detalhadas!

Todos os inputs serão apresentados abaixo, então, é muito importante que você consiga entender todos os passos que serão explicados. Se alguma etapa não tiver clara volte atrás e leia novamente. Vamos lá!

O arquivo de entrada é o setup.inp este arquivo possui as seguintes informações:

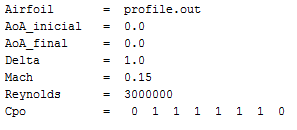
Airfoil é o nome do perfil que será criado durante a otimização, este nome não precisa ser alterado. Os valores de AoA_inicial e AoA_final precisam ser os mesmos e se trata do ângulo de ataque selecionado durante o processos de otimização. Delta consiste o incremento de ângulo de ataque entre o ângulo inicial e o ângulo final.

Esta variável não precisa ser alterada. Mach e Reynolds representam o número de Mach e número de Reynolds, respectivamente. Agora a variável Cpo consiste nos pontos de controle que serão alterados no processo de otimização. O perfil é parametrizado utilizando as curvas de Bézier, neste caso usando um polinômio de ordem igual a sete, e consequentemente com oito pontos de controle.

O número ‘1’ indica que o ponto será alterado já o número ‘0’ significa que o ponto ficará fixo em um valor pré-determinado. A imagem abaixo mostra o perfil de referência para o processo de otimização.

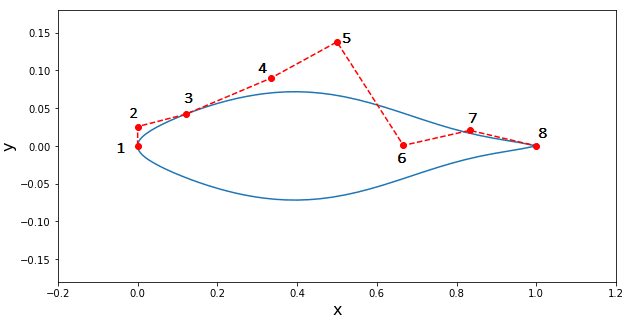
Tomando como exemplo os valores dados na figura anterior para a variável Cpo, temos que, o primeiro e último ponto estão fixos enquanto que os demais pontos podem ter a coordenada Y alterada pelo algoritmo de otimização. Como dito anteriormente o perfil é simétrico então à geometria do extradorso (parte superior) é espelhada no plano y para gerar o intradorso (parte inferior) do perfil. Vamos agora abordar pedaços do código que será modificado por você como parte deste exercício.

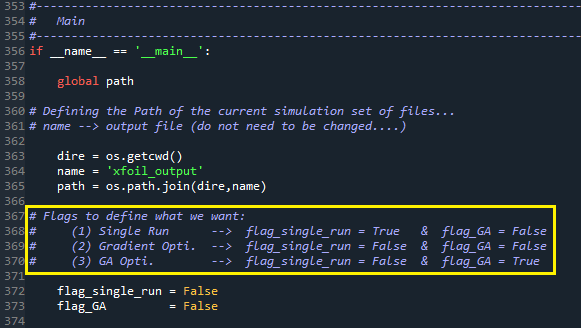
O programa Optimize_Profile.py tem uma função “__main__” que é o core do programa. Nesta parte do programa você precisa definir qual método de otimização você gostaria de utilizar ou se gostaria de realizar apenas uma análise simples com o XFOIL. O default do arquivo obtido no portal está para o método baseado em gradiente. Se quiser mudar para o SGA, que foi uma implementação que disponibilizei (GA_Class.py / GA_setup.py / Sobol.py) coloque flag_GA = True. Agora para a simulação simples apenas escolham flag_single_run = True.

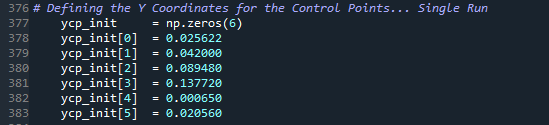
Algumas linhas mais abaixo “__main__” temos a definição dos pontos de controle que são necessários para gerar uma geometria inicial. Esta geometria inicial será utilizada em duas ocasiões. Na primeira ocasião quando você escolheu a simulação simples e na segunda quando você escolheu uma otimização utilizando o método de gradiente. A figura abaixo mostra um exemplo para o caso em que definimos 6 pontos de controle que serão utilizados para gerar esta geometria inicial. Esta definição segue a nossa escolha para a variável Cpo no arquivo setup.inp.

Por que temos 6 pontos de controle? Simplesmente porque na definição do Cpo colocamos seis valores com o índice ‘1’.

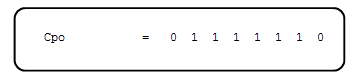
Temos que ter muito cuidado na definição dos índices do vetor que contém os dados para os pontos de controle. Se na definição de Cpo tivéssemos apenas dois pontos com o valor 1, ou seja, algo do tipo:

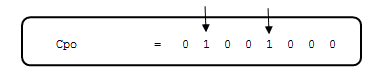
então, teríamos que definir ycp_init = np.zeros(2), onde ycp_init[0] = ‘valor 1’ e ycp_init[1] = ‘valor 2’. Note que o índice do vetor se refere à quantidade de pontos de controle que serão adotados e não a posição do ponto de controle. Ou seja, embora os pontos controle do vetor Cpo estejam nas posições ‘1’ e ‘4’ não devemos definir ycp_init[1] = ‘valor 1’ e ycp_init[4] = ‘valor 2’.

Apenas para verificar se ficou claro vamos supor que você deseja modificar os pontos de controle na posição 1, 3 e 5, então, a definição do código do vetor inicial no ficará ycp_init = np.zeros(3), onde ycp_init[0] = ‘valor 1’, ycp_init[1] = ‘valor 2’ e ycp_init[2] = ‘valor 3’.

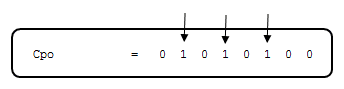
No método Optimization_Gradient é possível fazer modificações no setup do algoritmo de otimização.

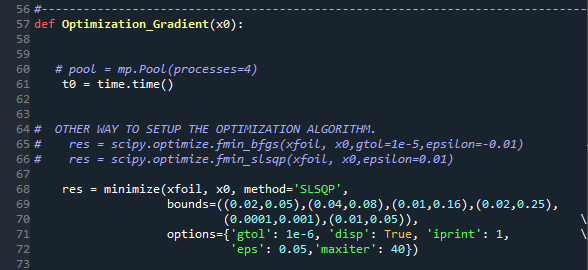
No campo method podemos escolher outros algoritmos disponibilizados pelo SciPy, entre eles:

Para maiores detalhes quando for alterar algum algoritmo busque a página abaixo. Alguns métodos demandam inputs adicionais, então, é importante saber estes detalhes caso contrário o código dará um “crash”, devido ao erro quando o algoritmo de otimização for acionado.

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html

Reparem que estes algoritmos irão buscar minimizar a função objetiva que você definiu! No caso deste exemplo estou passando para o otimizador o coeficiente de arrasto, Cd. Agora, se você quiser maximizar o coeficiente L/D, por exemplo, deve passar Obj = [1/ (L/D)], pois quanto maior o valor do L/D menor será a sua função objetiva. Assim, o otimizador buscará minimizar esta função objetiva procurando soluções que levem a valores elevados de L/D.

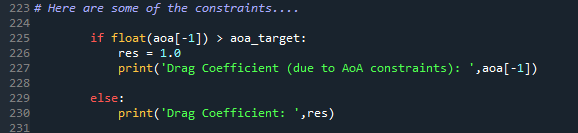
Como fazer alteração no código da função objetiva? No método xfoil do código Optimize_Profile.py temos o pós-processamento do resultado da simulação. A figura abaixo mostra os locais no código onde temos a atribuição de um valor a função objetiva do problema, aqui no código sendo representada pela variável ‘res’. Quando temos problema com a simulação o valor 1.0 é atribuído a ‘res’, quando a simulação ocorre sem problemas o atribuído é aquele obtido do arquivo de output.

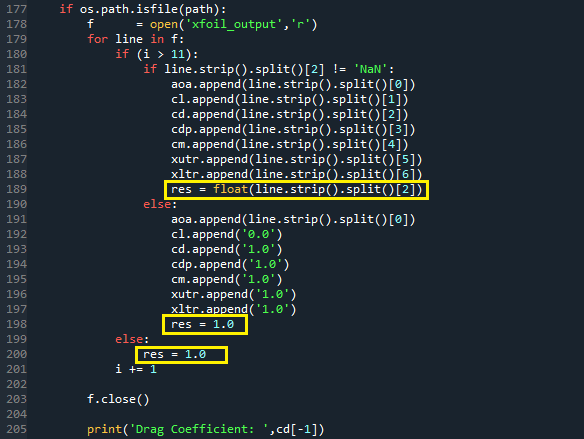
Notem que temos a seguinte ordem dos coeficientes:

(0:AoA, 1:Cl, 2:Cd, 3:Cdp, 4:Cm, 5:xtru, 6:xtrl)

Logo quando declaro o índice [2] na atribuição para ‘res’, estou indicando o coeficiente Cd para a função objetiva. No caso de uma otimização para maximizar o L/D o código seria alterado para algo como o descrito na imagem abaixo.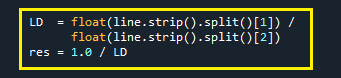

Agora, caso a sua escolha seja para o uso do algoritmo genético, SGA, não há necessidade de definir um vetor inicial para as variáveis, mas sugiro não alterar no “__main__” a definição do vetor ycp_init, pois ele não é passado para o GA. No entanto, será necessário definir parâmetros para o algoritmo de otimização. Este setup deve ser realizado no arquivo ga_setup.inp.

Onde as definições das variáveis são descritas como,

Generation – número de gerações na buscar pela melhor solução.

Population – número soluções (conhecidas como indivíduos) com que o otimizador trabalha de maneira simultânea.

Pmut – probabilidade de mutação de uma dada variável de projeto.

Pcross – probabilidade da realização do “cross-over” entre dois indivíduos que foram pareados.

Mating_Pool – Número de indivíduos que irão participar do “mating-pool”.

Type – o algoritmo pode trabalha com a representação binária ou real das variáveis de projeto.

BLX-alpha – parâmetro para a codificação real e que indica o coeficiente da distribuição de probabilidade para uma dada variável de projeto.

Var_size – consiste nu tamanho da string binária para representar uma determinada variável.

Variables – número de variáveis de projeto.

Var_Lower – limite inferior para as variáveis de projeto.

Var_Upper – limite superior para as variáveis de projeto.

A figura abaixo mostra a chamada do método que realiza a otimização com a implementação do SGA. Para executar esta otimização o método xfoil é passado para o método Opt_SGA do objeto ga.

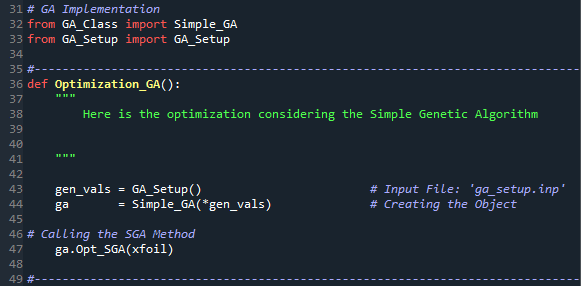
Se no futuro você tiver outra função que gostaria de otimizar, então, esta função deve ser passada para o método Opt_SGA. A figura abaixo exemplifica como executar a otimização com um método que consiste numa função analítica, mas também poderia ser um método que faz o setup para outro código, por exemplo, o SU₂. Notem que neste exemplo os métodos com a função analítica e os métodos para iniciar o algoritmo genético, GA, estão sendo chamados diretamente do “__main__”: . Isso é ligeiramente diferente do que você viu antes, mas o conceito é exatamente o mesmo! Não se esqueçam de que o arquivo setup.inp também deve ser atualizado com o novo número de variáveis e os limites das mesmas. Precisamos ter consistência com a nova função que está sendo chamada.

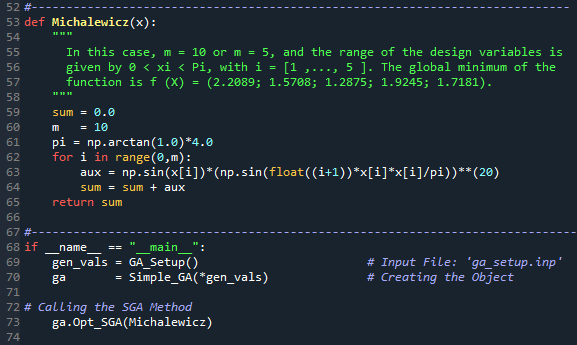
Os comentários feitos sobre alterações na função objetiva e explicados anteriormente para o método baseado em gradiente também valem para a otimização com o algoritmo genético. Ou seja, o mesmo método xfoil que está no código Optimize_Profile.py faz o pós-processamento dos resultados da simulação com o código XFOIL. A atribuição do valor a função objetiva se dá através da variável ‘res’.

ATENÇÃO: Um detalhe que não pode passar despercebido consiste no fato de que os GA’s são algoritmos que buscam obter o valor máximo de uma função. Assim, se você quiser minimizar a função objetiva, vamos supor o Cd, então, deve passar para o método do GA o valor Obj=1/Cd. Ou seja, algoritmo vai maximizar Obj buscando valore mínimos de Cd que é o que você deseja. Agora de você quiser maximizar o L/D, então é só passar Obj = L/D, simples assim! Não se esqueça disso!

Bem, até o momento não falamos da definição dos limites das variáveis de projeto para este estudo de caso. A tabela abaixo indica o limite inferior e superior que foi estipulado para os pontos de controle da parametrização Bézier.

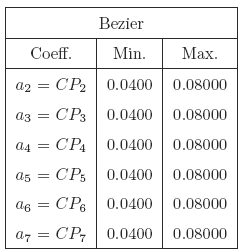
Já as duas imagens a seguir indicam a forma geométrica quando temos todos os pontos de controle com o valor mínimo e com o valor máximo que foi definido na tabela acima.

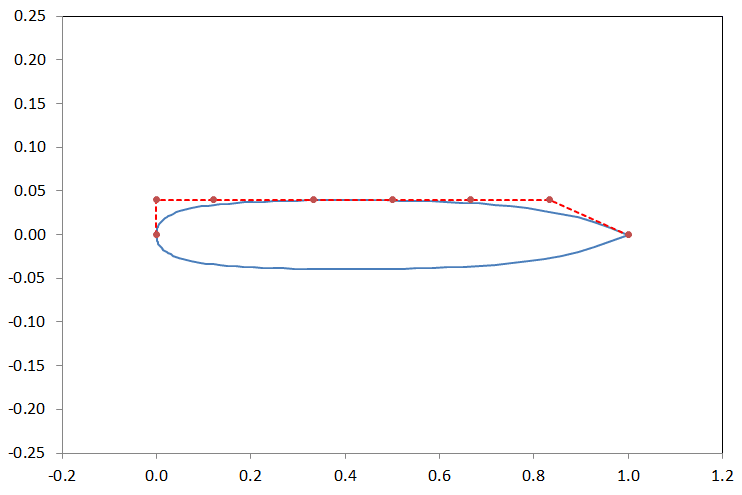
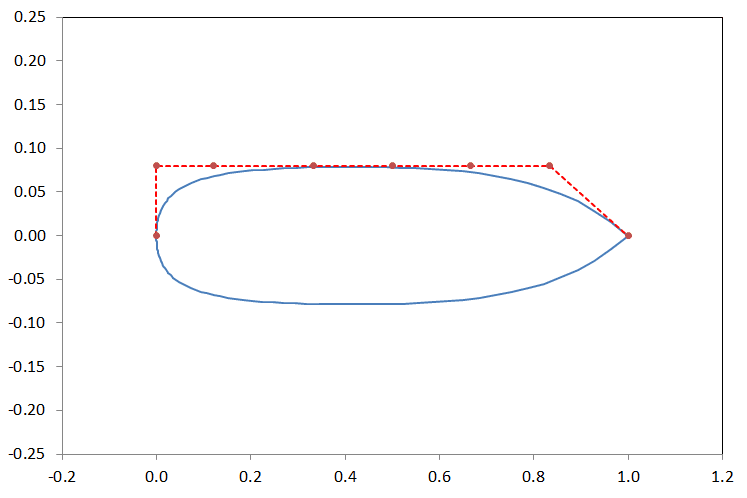
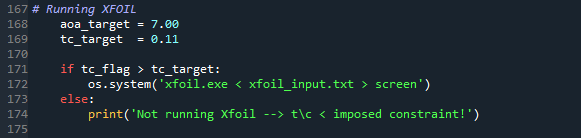
Um valor elevado para a função objetiva foi atribuído para todas as propostas geométricas que infringiam as restrições impostas tanto para a espessura relativa como para o ângulo de ataque. Sendo que, toda a vez que a espessura relativa era menor do que a restrição imposta, a simulação não era nem realizada. Simplesmente um valor alto para a função objetiva já era atribuído. No caso da restrição imposta para o AoA precisamos realizar a simulação para depois verificar qual o AoA obtido para se chegar ao Cl desejado. Se o AoA for maior do que a restrição um valor alto para a função objetiva é atribuído. As duas figuras abaixo mostram em que parte do código estas restrições foram impostas.

Os casos apresentados a seguir foram obtidos utilizando o SGA como o algoritmo de otimização. Basicamente, o que se apresentará é a influência da mudança dos parâmetros do algoritmo de otimização na solução final. O primeiro caso será tomado como a nossa referência e a partir do resultado obtido com este setup iremos avaliar o efeito da modificação dos parâmetros nas demais soluções. Abaixo temos a definição do setup de cada caso.

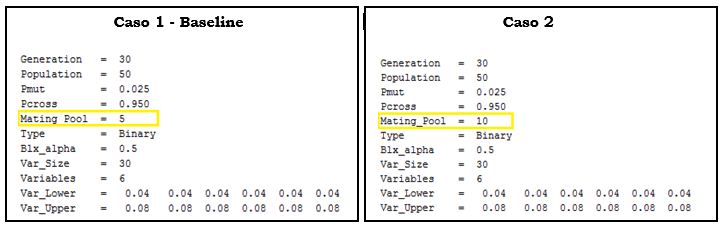
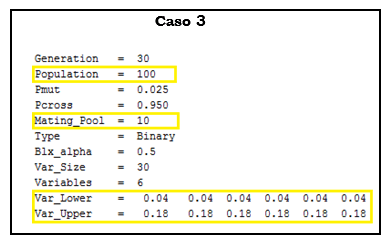
Nas figuras abaixo temos o histórico da evolução da função objetiva e o perfil ótimo para cada um dos casos avaliados. Podemos observar que no caso 2, quando aumentamos o valor da variável mating pool, foi possível obter uma solução com menor valor de arrasto. Neste caso considerando o mesmo número de gerações e tamanho da população.

Já no caso 3 foi mantido o valor de mating pool imposto no caso 2 e ainda se alterou o número de indivíduos para 100 e os valores do limite superior das variáveis de projeto. Podemos observar que estas alterações levaram a um valor de arrasto consideravelmente menor. Isso mostra como o setup do algoritmo afeta a resultado obtido e a necessidade de termos ciência de que o resultado obtido pode não ser o ótimo global.

A definição dos limites das variáveis de projeto limita o espaço de resposta e afetar os resultado obtido de maneira mais expressiva que o próprio algoritmo de otimização. Logo, fica claro como precisamos ter cuidado ao fazer afirmações que o resultado obtido é o ótimo global ou o método X é melhor do que o método Y, pois sempre introduzimos restrições neste processo de busca.

Case (1) – Mating Pool = 5, Population = 50, Cd = 0.00640

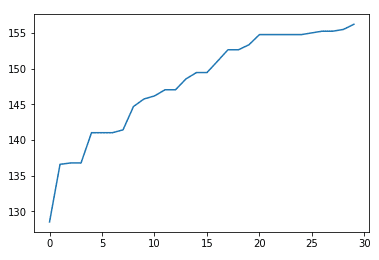
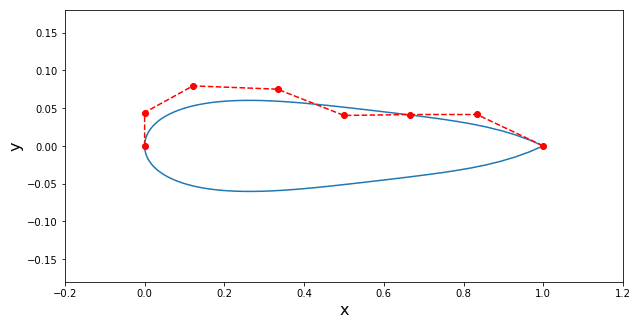
Case (2) – Mating Pool = 10, Population = 50, Cd = 0.00609

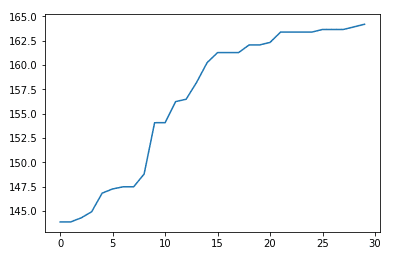
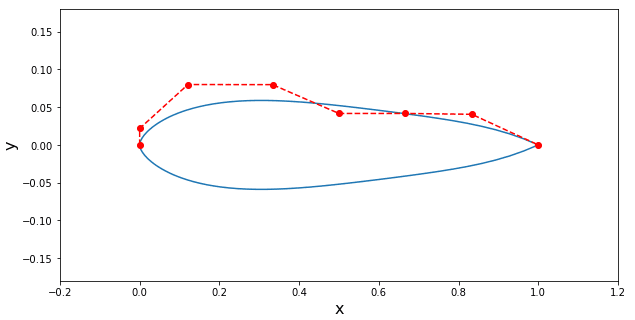
Case (3) – Mating Pool = 10, Population = 100, Cd = 0.00538

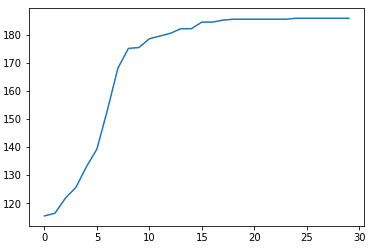
O tempo de CPU para o caso 2 foi de 50 minutos em uma máquina com processador Intel i3 e considerando a simulação realizada apenas com 1 processador. Realizando a otimização com o método SLSQP para este mesmo case 2 a otimização convergiu em 1minuto e 20 segundos para o valor de Cd = 0.00626.

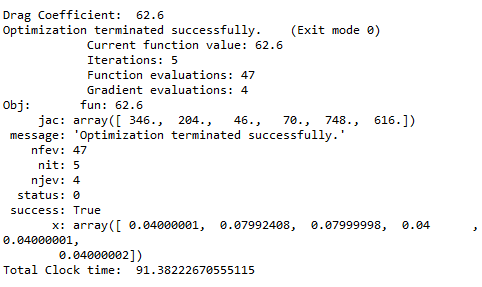
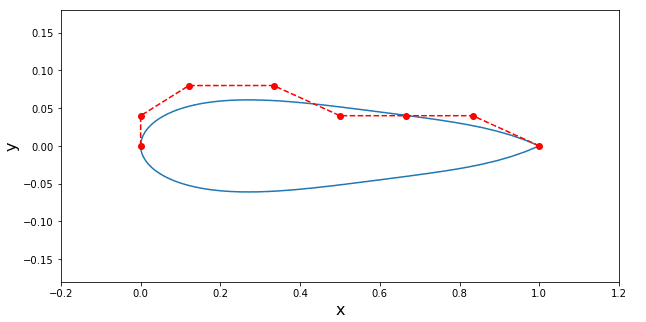
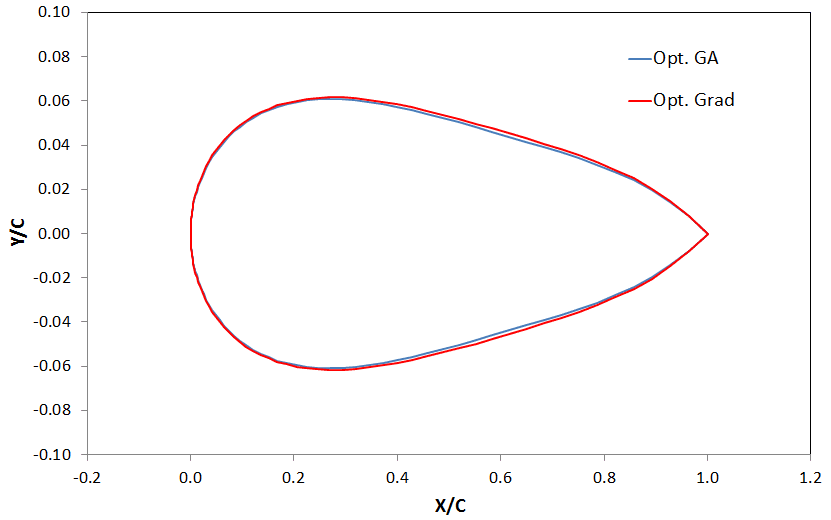
A figura abaixo mostra a diferença de geometria entre o resultado obtido com o GA e o obtido com o método de gradiente. Dá para notar que são muito próximas as duas geometrias. No entanto a diferença de tempo entre uma abordagem e outra é muito grande. Você acha que valeria a pena pagar esse custo computacional pelo delta de cd de 0.00017?

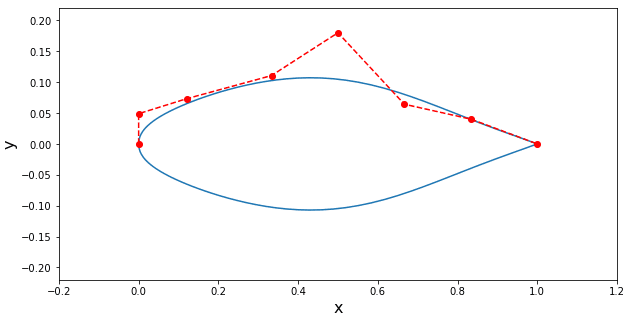
O resultado obtido com o método de gradiente partiu do perfil inicial mostrado quando foi explicado o setup dos pontos de controle do vetor Cpo. Um teste interessante consiste em partir do perfil obtido pelo algoritmo genético para ver que o método baseado em gradiente chega a uma solução ainda melhor. Faça este teste e veja se você consegue um perfil com menos arrasto. Você também pode fazer um estudo partindo de um perfil com arrasto muito ruim para verificar se o gradiente chega na mesma solução.

No curso veremos otimizações considerando um perfil que não é simétrico e a utilização do SU2 para você realizar as simulações com a formulação de Euler e Navier-Stokes. Além de outras otimizações considerando asa.

Arquivo para download: Projeto_Otimizacao_XFOIL

O que acha de conhecer mais lendo um artigo?

O Portal tem diversos conteúdos para te ajudar a se qualificar para o mercado de trabalho. Dê uma lida nesse artigo, depois conta pra gente o que achou!