Nível de dificuldade
Baixo
Curiosidades
Entenda a importância de elementos finitos na aviação
Escrito por
Rodrigo Martins
em 05 de novembro de 2018
Baixo
Você sabe o que é o método dos elementos finitos? Você sabe quais as principais aplicações e os principais desafios para o engenheiro de simulação numérica? Nesse post, gostaria de dar uma visão bastante geral sobre a história do método dos elementos finitos, definições básicas e as principais aplicações no projeto e análises de estruturas aeronáuticas.
Gostaria de iniciar esse post com uma frase famosa do renomado estatístico George Box:
“All Models are wrong,
but some are useful”
Filosoficamente falando, uma vez que todos os modelos baseiam-se na percepção humana, que é limitada, eles estão sempre em certo grau errados. Um cientista nunca poderá obter um resultado exato por elaboração excessiva do seu modelo, qualquer ele que seja.
Pelo contrário, o pensamento científico deve buscar sempre uma explicação mais simples possível para os fenômenos. O mesmo vale para os modelos de engenharia. Se dois modelos tem o mesmo nível de representatividade, aquele que for mais simples é mais adequado.
Outra frase famosa em escritórios de engenharia que é bom todo jovem engenheiro ir se acostumando:
FEM ≠ Análise Estrutural
Isso já faz sentido a priori, uma vez que o método dos elementos finitos é um método aproximado para solução de equações diferenciais. No sentido prático, isso é uma forma de atentar que o software faz os cálculos , mas é o engenheiro quem faz a análise.
Matematicamente falando, sabe-se que o método dos elementos finitos é um método aproximado para solução de equações diferenciais. Quando se fala em elementos finitos já associamos análise de estruturas, mas, ele pode ser utilizado para diversas aplicações, como mecânica dos fluidos, eletromagnetismo, etc. Essa associação veio das primeiras aplicações serem para solução de problemas de mecânica dos sólidos.
Na prática, a frase “Elementos finitos não é análise Estrutural” quer dizer que os cálculos que os programas de elementos finitos fazem são meras ferramentas para que o engenheiro faça a análise estrutural. A análise sempre requer julgamento de engenharia e bom senso. Inclusive, a análise dos resultados pode indicar erros no modelamento da estrutura.
O portal Engenharia Aeronáutica foi criado justamente para que esse julgamento de engenharia, essa experiência, possa ser difundida na comunidade de engenheiros do Brasil. Tendo isso em vista, a sua participação, com comentários, dúvidas, sugestões, é muito importante para o crescimento do portal.
O método dos elementos finitos foi desenvolvido paralelamente em diversas partes do mundo, tendo como base o cálculo variacional. Após a segunda guerra mundial, uma grande corrida tecnológica se iniciou e os primeiros resultados práticos foram obtidos por Alexander Hrennikoff do MIT e Richard Courant da NYU.
No início da década de 60, a então jovem NASA iniciou um grande projeto de um software que pudesse resolver seus problemas de mecânica dos sólidos de maneira genérica. Foi o início do projeto NASTRAN(NASA STRUCTURAL ANALYSIS)
No final da década de 70, no MIT, o professor Klaus Bathe, criou o software ADINA, capaz de resolvez problemas com não-linearidades complexas, como contato , deformações severas, etc. Esse programa foi posteriormente incorporado ao NASTRAN. No final da década de 70 a NASA, através da empresa MSC disponibilizou uma versão comercial do NASTRAN para ser utilizado por empresas.
Figura 1 – Evolução dos softwares de elementos finitos nos estados unidos
Em 2001, a NASA liberou o código fonte de uma versão básica do NASTRAN e logo depois em 2002, devido a leis americanas anti-trust, a empresa MSC teve que vender para a Siemens parte de sua empresa. Hoje existem 3 versões diferentes do NASTRAN, o NX-NASTRAN(Siemens), o MSC-NASTRAN(MSC) e o Nei-NASTRAN(Nei).
No histórico dos programas de elementos finitos, o NASTRAN se destaca, principalmente porque ele foi utilizado desde sua concepção na indústria aeroespacial. Portanto, os órgãos homologadores ainda tem uma confiança maior nos resultados obtidos pelo NASTRAN do que os obtidos em outros softwares.
Um curso básico de elementos finitos duraria pelo menos 60 horas de aulas expositivas. Entretanto existe um curso teórico bastante completo e abrangente é oferecido pelo MIT gratuitamente no link:
Fundamentalmente falando, o método dos elementos finitos, é um método de solução de equações diferenciais que se utiliza de funções para solução, cuja forma (em geral polinomial) é conhecida a priori, e, através de uma transformação integral, o problema diferencial é transformado em um problema algébrico em um domínio discreto.
Figura 2 – Aplicação do princípio dos trabalhos virtuais para implementação do método dos elementos finitos.
Vamos ilustrar a aplicação do problema através de um exemplo simples de uma barra tracionada.
Figura 3 – Problema de uma barra carregada axialmente
Fazendo o diagrama de corpo livre de um segmento infinitesimal da barra, tem-se:
Figura 4 – Diagrama de corpo livre de uma estrutura infinitesimal de uma dimensão.
A partir do diagrama de corpo livre, o somatório de forças fica sendo:
Dividindo por Δx e tendendo esse valor a zero, tem-se:
Utilizando a lei de Hook:
Substituindo na equação de equilíbrio:
Essa é a equação diferencial do sistema estrutural.
As condições de contorno para esse caso específico são:
Toda condição de contorno em deslocamento é dita essencial e toda condição de contorno em força ou tensão é dita natural.
Vamos agora criar um elemento finito que descreva essa barra:
Para esse elemento vamos supor uma função de interpolação linear:
O elemento está representado abaixo:
Figura 5 – Elemento finito uniaxial de dois nós
Essa interpolação pode também ser escrita como:
Onde u1 e u2 são os deslocamentos nodais e N é a função de forma do elemento na forma vetorial.
Uma vez que:
Portando:
A deformação é portanto:
As tensões pela lei de Hook:
Aplicando o princípio dos trabalhos virtuais:
Ao se aplicar um deslocamento virtual , o trabalho realizado pela força real e o deslocamento virtual é igual ao trabalho interno realizado pelas tensões reais e as deformações virtuais. Isso significa que:
Mas as deformações virtuais são função dos deslocamentos virtuais:
Substituindo o valor da deformação na equação de equilíbrio dos trabalhos:
Expandindo as tensões e as forças nos nós 1 e 2:
Desenvolvendo:
Uma vez que a relação deve ser nula para um deslocamento virtual qualquer, segue que:
Resolvendo:
Portanto, transformou-se a equação diferencial em um sistema de equações lineares. A matriz que multiplica os deslocamentos é chamada de matriz de rigidez.
Note, que um dos deslocamentos precisa ser prescrito, já que a matriz de rigidez é singular. Para o exemplo que estamos resolvendo o deslocamento no nó 1 é nulo. Fisicamente isso pode ser entendido como condição essencial para não existência de movimento de corpo rígido.
A seguir segue um problema resolvido com o elemento finito de dois nós desenvolvido:
Note que como o carregamento varia linearmente, as tensões não são contantes na barra, portanto, são necessários de mais elementos para representar corretamente os deslocamentos na barra.
Essa é uma introdução bastante simplificada da formulação do método. Para quem tem pouca ou nenhuma experiência, eu sugiro o livro: Um primeiro curso em elementos finitos do Jacob Fish. Para quem quer se aprofundar no assunto e quer um livro mais completo, eu sugiro o Finite Element Procedures do Bathe ou o Structural Analysis with the Finite Element Method do Eugênio Oñate.
A seguir é mostrado o modelo global de uma asa. Esse tipo de modelo possui sua geometria bastante simplificada e a aplicação de carregamentos também é simplificada. Mas não se engane, o modelo não necessariamente precisa ser geometricamente representativo para ser estruturalmente representativo. Esse é o grande desafio dos modelos globais: representar o comportamento de uma grande estrutura sem a utilização de muitos elementos.
Figura 6 – Modelo global de uma asa genérica
Os resultados desse tipo de modelo são esforços internos para sub-componentes. Muitos deles são analizados por métodos semi-empíricos, como Lugs, painéis reforçados, Juntas de tração, etc.
Outras estruturas, como ferragens de fixação, pilone, e até nervuras necessitam de um modelo detalhado para sua análise. A união do modelo entre modelos globais e detalhados é feita utilizando-se técnicas globais/locais. Essas técnicas incluem criação de:
Figura 7 – Modelo de uma ferragem de fixação.
De maneira bem simplificada, a análise de flambagem é obtida através da solução de um problema de auto-valor:
A margem de segurança se relaciona com o menor auto-valor da seguinte forma:
Figura 8 – Resultado de Flambagem de uma nervura.
Os modos de vibração da estrutura também são obtidos através da solução de um problema de auto-valor:
Figura 9 – Análise modal de uma membrana.
Existem vários tipos de otimização estrutural. Os principais são:
Onde cada variável do problema de otimização corresponde a uma espessura ou comprimento de um elemento ou propriedade.
Figura 10 – Resultado de uma otimização de tamanho no revestimento de uma asa
Otimização que visa aumentar a rigidez a uma estrutura sem acrecentar massa simplesmente mudando sua topografia. Muito utilizada para peças estrampadas, onde o ressalto pode ser feito facilmente.
Figura 11 – Otimização topográfica
Dá uma noção ao engenheiro do melhor caminho de carga possível. Algumas indústrias já estão conseguindo fazer com que a otimização topológica seja utilizada do início ao fim do projeto, mas essa tecnologia ainda está no estado da arte.
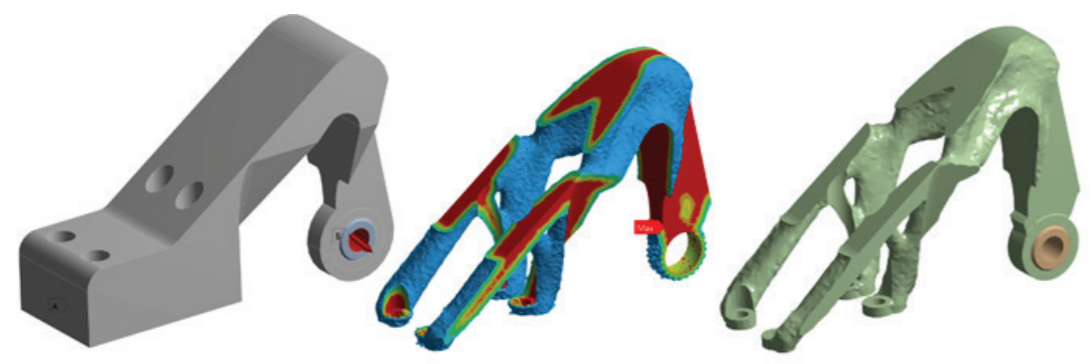
Figura 12 – Otimização topológica
Existem métodos numéricos bastante consagrados para obtenção de parâmetros de mecânica da fratura (tais como fator de intensidade de tensão e integral J) e alguns softwares disponíveis no mercado. A seguir é mostrado um software que para cada intervalo de tempo, ele calcula os parâmetros, calcula a direção e tamanho do crescimento da trinca.
O SouthWest Research Institute desenvolve constantemente em parceria com diversas empresas inclusive a Nasa, um software baseado em equações semi-empíricas para o crescimento de trincas em geometrias típicas de sub-estruturas de aeronaves. Dessa maneira, tudo que é necessário como input para o programa seria um espectro de tensão, que todos os fatores de intensidade de tensão são calculados para as geometrias que o software possui. Vou incluir um link para esse centro de pesquisa.
São basicamente duas maneiras de resolver o problema, mas como utilizar elementos finitos em toda a etapa de obtenção dos parâmetros de mecânica da fratura tende a ter resultados piores do que resultados baseados na em vários tipos de geometria reais e um carregamento genérico.
O requisito 571 da ANAC exige que a aeronave seja segura mesmo sendo submetida a cargas acidentais, como é o exemplo de um impacto de pássaro. Existem outros tipos de cargas nesse requisito, como despalhetamento de motor, e existe modelo de elementos finitos pra isso também. Pelo fato de essas análises serem mais complexas, são também exigidos ensaios. E um modelo desse tipo, exige muita experiência do engenheiro, para que o modelo corresponda ao ensaio. Um ensaio mal sucedido pode custar milhares ou milhões de dólares de prejuízo.
Segue uma análise de impacto de pássaro feita em LS-DYNA:
O que acha de conhecer mais lendo um artigo?
O Portal tem diversos conteúdos para te ajudar a se qualificar para o mercado de trabalho. Dê uma lida nesse artigo, depois conta pra gente o que achou!
Quer conhecer mais sobre o Portal Engenharia Aeronáutica?
▶ INSCREVA-SE no nosso canal do Youtube! Vem com a gente e embarque no mundo da aviação!
https://www.youtube.com/c/EngenhariaAeronáutica?sub_confirmation=1
Siga a gente nas redes sociais!
▶ Facebook: https://www.facebook.com/engenhariaaeronauticabr/
▶ Instagram: @engenhariaaeronautica (https://www.instagram.com/engenhariaaeronautica/)
