Nível de dificuldade
Baixo
Curiosidades
Um Resumo Sobre Confiabilidade
Escrito por
Sergio Duarte
em 25 de setembro de 2018
Baixo
Confiabilidade, conhecida mais popularmente pela letra R (do Ing.: Reliability), é uma função complementar de uma distribuição cumulativa de probabilidades, conhecida pela sigla CDF (do Ing.: Cumulative Distribution Function), denominada Falibilidade (Ing.: Unrealibility), representada pela letra F (derivada do inglês Failure).
F aponta para cada intervalo de tempo t a probabilidade de um item falhar naquele intervalo. R, por ser sua função complementar, indica a probabilidade do item não falhar nesse intervalo.
A CDF mais utilizada em aviação é a exponencial negativa, dada por:
R = e-λt (1)
que resulta de:
R = 1 – F = 1 -(1-e-λt) (2)
e t é uma variável aleatória contínua e λ é uma constante denominada taxa de falha.
(1) e (2) nos informam que para t=0, R = 1 e F = 0. Para t muito grande, R tende a zero e F tende a 1.
A exponencial negativa tem uma propriedade interessante, conhecida por Propriedade do Esquecimento ou da Perda de Memória. Com isso queremos dizer que quando o item que segue essa função é desligado e ligado novamente, tudo se passa como se estivesse começando a operar pela primeira vez, ou seja, o item não se “lembra” de ter operado antes.
Na prática a CDF (1) aplica-se, com boa aproximação, a itens elétricos e eletrônicos, porque a taxa de falha desses itens é aproximadamente constante, na fase operacional, depois que o projeto desses itens estiver maduro. Com o passar do tempo, que varia de item para item, a taxa de falha deixa de ser aproximadamente constante e começa a crescer com rapidez. É a fase do desgaste.
É importante assinalar que a confiabilidade depende do item e das condições do evento a que é submetido. Por esse motivo é que nos requisitos de confiabilidade do projeto de um item não é suficiente citar um valor de confiabilidade. Portanto é preciso especificar as condições em que ocorre o evento.
Isso é muito importante para evitar discussões estéreis, depois que o item entra na fase operacional. Uma aeronave civil segue eventos mais ou menos bem definidos, voando sempre na mesma configuração, isto é, rolagem na pista, decolagem, subida, cruzeiro, descida, aterragem, rolagem na pista e pronto. Já os aviões militares, têm configurações de missão diferentes e é comum, durante o adestramento em Bases Aéreas, o piloto variar configurações. Desse modo, é comum também os militares se queixarem da confiabilidade da aeronave, quase sempre abaixo daquela de requisito. Inclusive, o normal, nos projetos militares, é estabelecer um requisito de confiabilidade para a missão mais comum.
O que se faz então, na prática militar, é procurar aperfeiçoar a confiabilidade, na fase operacional, adotando processos de melhoria, como por exemplo o método de aperfeiçoamento da confiabilidade de Duane.
Em se tratando de itens elétricos e eletrônicos reparáveis, o inverso de λ é outra constante denominada MTBF (do Ing.: Mean Time Between Failures).
Existe, por parte de alguns, uma confusão com os parâmetros MTBF e MTBUR (do Ing.: Mean Time Between Unscheduled Removal). O MTBUR inclui todas as remoções do item, com pane constatada ou supostamente em pane, ao passo que o MTBF se refere somente a remoções com panes constatadas. É comum o pessoal de manutenção, no início da operação, isto é, sem muita prática com o sistema (e isso já vivemos bastante), remover itens, achando que estejam em pane. Evidentemente, o MTBUR é menor que o MTBF, ou seja, a taxa de remoções é maior que a taxa de falhas e, quase sempre, essa diferença é grande, sobretudo no início das operações. Obviamente, o MTBUR é variável, tendendo, com o tempo, a ser igual ao MTBF.
A figura a seguir apresenta as famosas curvas da Confiabilidade e Fabilidade. É fácil ver que quando maximizamos R, minimizamos F. É o que se procura fazer nos projetos. Mas esse processo tem limites ditados por custos, espaço e peso. Dessa forma, uma melhora centesimal da confiabilidade pode significar um acréscimo de milhões de dólares no custo.
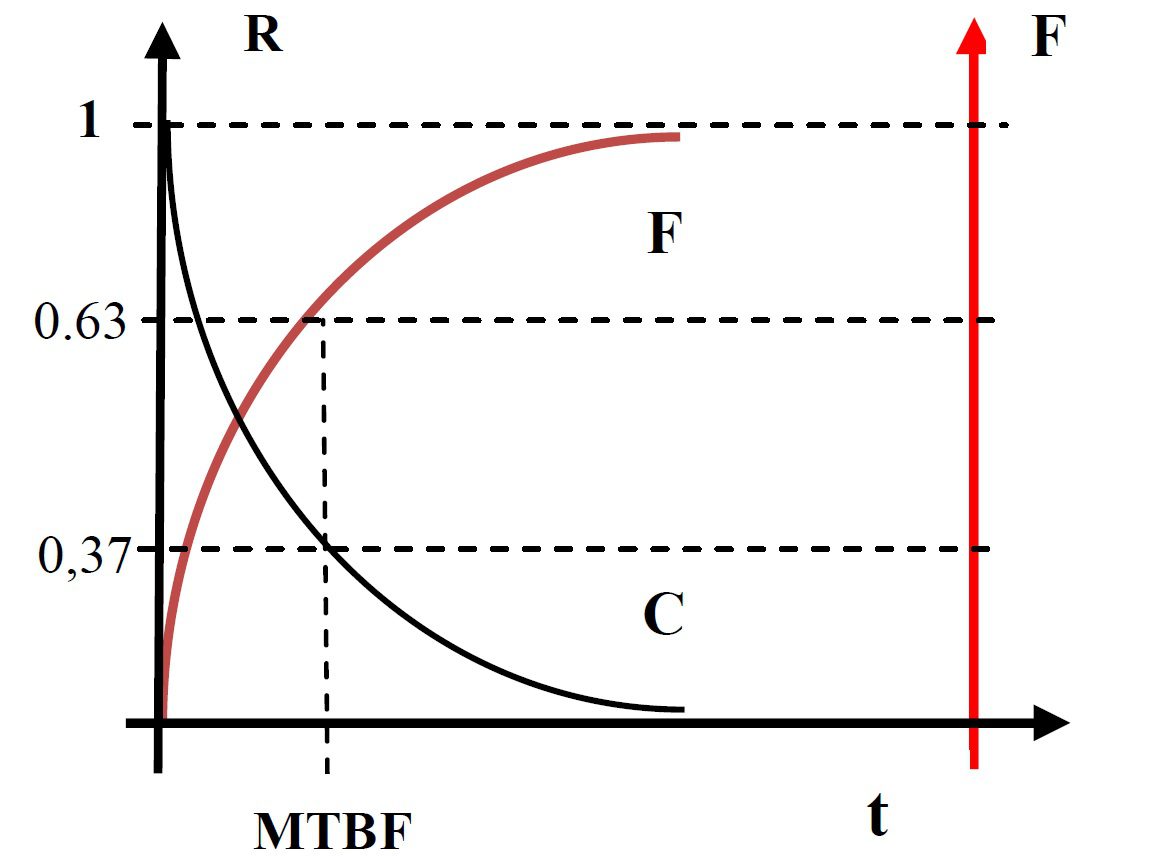
Naturalmente, se conhecermos λ para um determinado item, teremos a expressão (1) para o mesmo. λ é obtido por meio de testes cujos resultados são inseridos na expressão (3).
λ=número de falhas/tempo total de operação (3)
O problema é determinar o tempo total de operação. Isso porque podemos fazer testes com um só item ou com vários ou com ou sem substituição dos itens falhados. Vejamos um exemplo rápido com um só item.
Suponhamos que o ciclo de operação (um ano) para um dado item eletrônico seja de 187,5 horas, como mostrado na figura abaixo. Durante esse tempo, ocorrem falhas nos momentos indicados na figura abaixo:
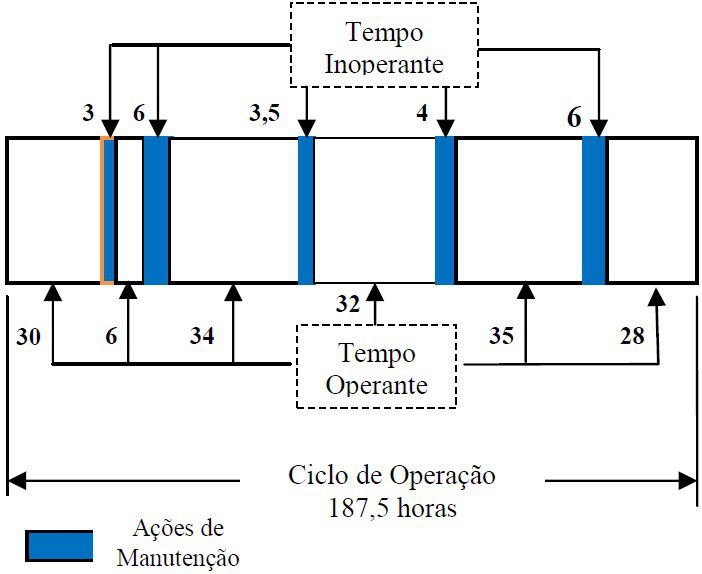
Ciclo de Operação de 187,5 horas, tempo de Operação de 165 horas, e tempo Inoperante de 22,5 horas.
Portanto, trata-se de um ensaio de 165 horas com 5 falhas. Desse modo, a expressão (3) fica:
λ = 5165 =0,03h-1
Então, o valor apurado em (4) aplicado à expressão (1) nos daria:
λ = e-0,03t
Esse foi o primeiro passo para o entendimento acerca do processo de Avaliação de Segurança (Safety Assessment).
Aproveitem para ler também sobre o que é necessário para projetar uma aeronave ou sobre Ensaios Ambientais de Sistemas Aviônicos!
Até breve!
Berquó, Jolan Eduardo – Eng. Eletrônico (ITA)
Certificador de Produto Aeroespacial (CTA/IFI)
Representante Governamental da Garantia da Qualidade – RGQ (DCTA/IFI)
(1) MODARRES, M. Reliability and Risk Analysis. Cincinnati – Ohio (EUA): Marcek Dekker, Inc., 1993.
(2) BLANCHARD, Benjamin. S – FABRICKY, Wolter J. Systems Engineering and Analysis. 4. Ed. EUA (3) DoD: MIL-STD-785B, Reliability Program for Systems and Equipment. EUA Department of Defense, Washington, D.C.
(4) O’CONNOR, P.D.T. Practical Reliability Engineering. John Wiley & Sons, Inc., New York, 1991.
