
Baixo
Curiosidades
Safety Assessment – Discorrendo sobre a AC 25.1309 (II/IV)


Baixo

Após a leitura do primeiro post sobre a AC 25.1309-1A, vamos tratar, nesta oportunidade, do binômio: severidade da condição de falha e faixa de probabilidade permissível para a severidade nos moldes do Safety Assessment.
Primeiramente, é necessário ter em mente que não existe avião à prova de acidente fatal. Probabilidade zero de ocorrência desse tipo de acidente é mera quimera. Podem-se usar milhares de redundâncias para um sistema e, ainda assim, a probabilidade de acidente fatal não é nula. Além de tal prática poder levar os custos de projeto às alturas.
Por isso, foi necessário estabelecer um aceitável nível de segurança (Acceptable Safety level). Esse nível, na aviação civil, decorreu do que se intitulou de taxa aceitável de acidentes (Acceptable Accident Rate).
Essa taxa derivou da análise da taxa de acidentes de toda a frota de aviões comerciais ocidentais, no período de 1970 a 1980. Observou-se que, nesse período, a taxa de acidentes catastróficos foi pouco menor que 1 x 10-6.
Em números:
Onde NC é o número total de acidentes catastróficos.
Considerando a grande quantidade de horas envolvidas (106), o valor acima pode ser considerado como probabilidade, obtida segundo o conceito empírico de probabilidade:
Supondo que 106 horas seja um número suficientemente grande, onde:
No entanto, a análise das causas desses acidentes evidenciou que apenas 10% foram causados por falhas de sistemas. Em números:
onde NS é o número de acidentes atribuídos a sistemas, e N0 é o número de acidentes atribuídos a outros itens.
Desse modo, a parte atribuída a sistemas foi:
Partindo de uma hipótese arbitrária, estabeleceu-se que uma grande aeronave comercial poderia apresentar cerca de 100 potenciais condições de falhas catastróficas atribuíveis a sistemas. Desse modo, ter-se-ia um subconjunto de eventos do espaço amostral das condições de falhas catastróficas constituído por 100 eventos. Cada um para cada condição de falha catastrófica atribuível a sistemas. Poder-se-ia então representar tal subconjunto por:
onde Ci é um evento catastrófico genérico atribuível a sistemas.
Teríamos então .
Admite-se que C seja um conjunto equiprovável, ou seja, que cada um de seus 100 eventos tenha a mesma probabilidade de ocorrência. Rigorosamente, isso não é verdade. Mas tendo em conta que para nossa análise o interesse está na faixa atribuída a cada severidade, podemos considerar um único e genérico valor representativo de probabilidade para cada evento de cada faixa. Neste caso, é a faixa dos eventos catastróficos. Sendo assim, teríamos:
Resultando então em:
Portanto, , ou o famigerado número conhecido:
.
Esta é a faixa registrada na AC, para as condições de falha Catastrófica.
Uma vez estabelecido esse valor máximo do intervalo aberto de probabilidade, para as condições de falhas catastróficas, foram estabelecidos também os outros limites máximos de intervalos para as demais severidades. Não temos informações de que esses limites tenham se baseado em dados históricos ou se foram arbitrados.
Com base nos resultados numéricos acima, a AC estabelece então, para a condição de falha Catastrófica, a faixa de probabilidade P<10-9. Em consequência, essa é a faixa de valores que o item (b)(1) do § 25.1309 diz que tem de ser extremamente improvável.
Já a condição de falha Maior, que o item (b)(2) do § 25.1309 estabelece que tem de ser improvável, a AC a situa no intervalo aberto de probabilidade 10-9<P<10-5.
Finalmente, para a condição de falha Menor, a AC a situa na faixa P>10-5, estabelecendo para os valores aí contidos o nível provável. Esta condição de falha não é enquadrada no § 25.1309 porque é aceitável que ocorra.
É importante observar que a AC estabelece também duas possibilidades para o enquadramento na severidade Maior, uma mais grave que a outra. Fala de uma severidade, digamos, Maior Normal, ou simplesmente Normal, e de uma severidade Maior Severa. Esses dois casos estão enquadrados, sem distinção na AC, na já mencionada faixa de probabilidades 10-9<P<10-5.
Com relação a esse detalhe da severidade Maior, registra-se que a AC 23.1309-1E, para pequenos aviões, e a AMC 25.1309, da EASA, para grandes aeronaves, denominam as duas condições de severidade Maior da AC 25.1309- 1A de Maior e Perigosa (Hazardous), caracterizando-as da seguinte maneira:
Não vemos nenhum problema se o requerente quiser usar essa nomenclatura.
É interessante apresentar um exemplo para que se tenha uma ideia da lógica dos números acima. Uma aeronave pode voar cerca de 5 x 104 horas, em sua vida útil. Então, uma grande frota de 200 aeronaves do mesmo tipo pode acumular um total de 107 horas. Não se espera, portanto, que ocorra uma falha Catastrófica (P<10-9), nesse período.
Já a condição de falha Maior (10-9<P<10-5), pode acontecer uma vez na vida de uma aeronave e várias vezes na vida da frota.
Finalmente, a condição de falha Menor (P>10-5) pode acontecer várias vezes na vida da aeronave.
Nosso próximo passo, agora, é dar uma ideia do procedimento para realizar uma Safety Assessment. Com o objetivo de facilitar a tarefa do requerente, a AC presenta um diagrama de fluxo (mostrado abaixo), procurando orientar o requerente em sua avaliação de segurança. Mas esse diagrama será tratado, passo a passo, nos próximos posts sobre Safety Assessment.
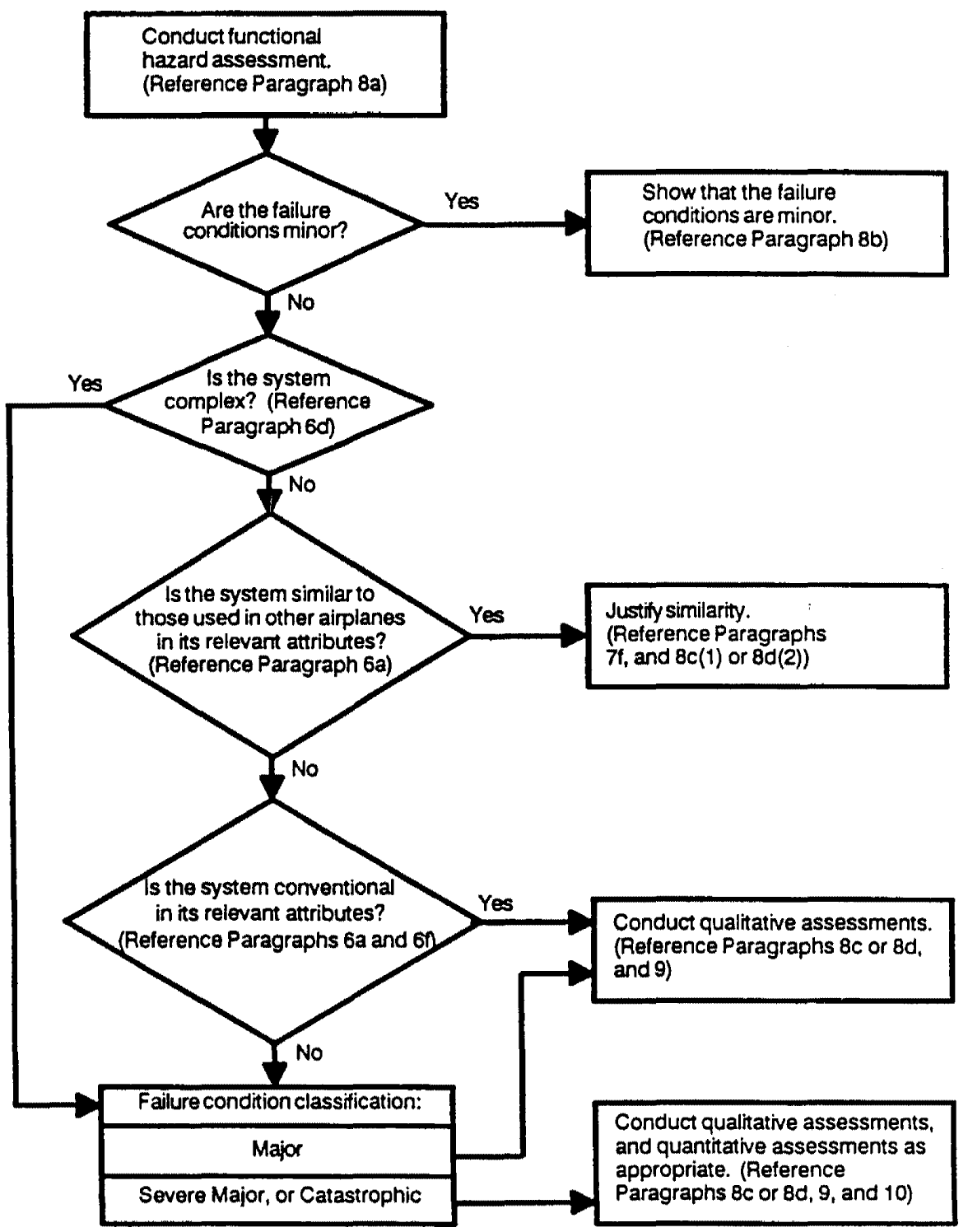
Fique ligado e até a próxima!
(1) FAA: CFR 14 Part 25 § 1309, Equipment, Systems, and Installations, Amendment 25-123, EUA, 8/11/2007.
(2) FAA: AC 23.1309-1E, System Safety Analysis and Assessment for Part 23, EUA, 17/11/2011.
(3) FAA: AC 25.1309-1A, System Design and Analysis, EUA, 21/06/1988.
(4) EASA: AMC 25.1309, System Design and Analysis. CS-125 – Book 2, Amendment 6, Colônia (Alemanha), 6/7/2009.
(5) De Florio, Filippo. Airworthiness – An Introduction to Aircraft Certification. 2nd. ed. EUA: Elsevier Ltd, 2011.