
Baixo
Artigos
Algoritmos de Otimização


Baixo

Pessoal, neste artigo iremos falar muito rapidamente sobre a importância da simulação numérica e os Algoritmos de Otimização. Posteriormente, como devemos estabelecer um problema de otimização e alguns dos importantes conceitos sobre os algoritmos. Então vamos lá!
Uma vez que foi apresentado um conceito sobre a parametrização geométrica do perfil, vamos agora falar do próximo passo o qual consiste na análise numérica. O processo de análise numérica pode variar de poucos segundos até mesmo muitas horas. Tudo depende da formulação das equações governantes que foram selecionadas para a realização da simulação numérica. Estes conceitos podem ser vistos no módulo de CFD que estará disponibilizado neste Portal.
Neste momento, lembrem que a análise numérica é fundamental para obtenção das principais informações sobre os coeficientes aerodinâmicos globais e as características da topologia do escoamento. Para isso é importante conhecermos a formulação das equações governantes e o que significam as simplificações nestas equações. Neste módulo de projeto e otimização a simulação numérica será tratada como uma caixa preta.
A seguir apresentarei alguns dos principais conceitos sobre otimização:
A otimização consiste em um conjunto de atividades/operações através da qual se busca obter a melhor solução para o projeto de interesse. Note que esta frase precisa ser mais bem contextualizada, caso contrário fica muito vago o significado do termo melhor solução de projeto. Isso mostra a importância da definição do problema de otimização, ou seja, a definição da função de mérito, das restrições de projeto e do intervalo das variáveis de projeto.

Abaixo temos um exemplo de um ‘statement’ de otimização. Podemos verificar qual a função de mérito ou função objetiva e se o problema é de maximização ou minimização. Também podemos verificar a parametrização que será adotada e quantas variáveis de projeto serão consideradas, assim como as informações das condições de voo e as restrições geométricas.
Em particular este ‘statement’ diz que desejamos minimizar o arrasto de um perfil considerando a parametrização de Bézier para a condição de voo de Mach=0.15, Cl=0.45 e número de Reynolds de 3 milhões. O ângulo de ataque está restrito entre os limites [-3,3] graus, dado que buscamos um Cl constante e o otimizador pode variar o ângulo de ataque. Também podemos ver uma restrição geométrica que define que o valor de t/c deve ser maior do que 11%. Tem alguma informação faltando na definição desta otimização?

A resposta é sim! Embora o ‘statement’ esteja claro ele não está completo. Falta definir qual o range das variáveis de projeto, o código que será adotado para executar as simulações numéricas e o algoritmo de otimização com o setup dos parâmetros. Após prover todas estas informações adicionais a análise estará perfeitamente descrita! Não restará qualquer dúvida sobre o que se busca e esta plenitude de informação possibilitará que o seu resultado possa ser reproduzido por outras pessoas.
O exemplo acima aborda apenas uma disciplina que é a aerodinâmica, agora imagine a definição de um problema de otimização multidisciplinar onde temos várias disciplinas envolvidas. Dada à quantidade de funções objetivas, variáveis de projeto e restrições de diversas naturezas o problema ganha uma considerável complexidade. Logo, faz-se necessária uma definição cuidadosa do ‘statement’ da otimização.
Os algoritmos de otimização podem ser classificados em duas grandes categorias: aqueles que baseiam o seu processo de busca utilizando o gradiente da função objetiva e os métodos estocásticos. Vamos descrever logo a seguir alguns dos principais conceitos destas duas possíveis abordagens, mas antes disto a Tabela abaixo mostra algumas características de cada uma destas abordagens.
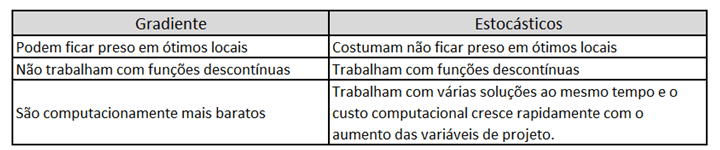
Exemplos de métodos baseados em gradiente são: Nelder-Mead, Powell, CG, BFGS, Newton-CG, L-BFGS-B, TNC, COBYLA, SLSQP entre outros. Já alguns dos exemplos de métodos estocásticos são: Hill-climbing, Simulated annealing, Evolutionary algorithms and Genetic Programming, Particle Swarm Optimization, Ant Colony Optimization.
Para os métodos baseados em gradiente o processo de otimização se inicia a partir de um ponto inicial. A busca é realizada a partir de uma direção no espaço de resposta e um valor escalar que define a distância que andaremos nesta direção.
![]()
Onde é um escalar que define o quanto andamos na direção definida por e é a solução corrente. O valor de vai aumentando enquanto a função objetiva estiver diminuindo e as restrições não estiverem sendo violadas. Notem que o processo de busca usando uma direção específica transforma o problema que era de n variáveis em um problema de apenas uma, que é a variável . Os métodos que usam esta formulação para efetuar a busca são chamados de métodos de primeira ordem. Já os métodos que usam a segunda derivada da função S são chamados de métodos de segunda ordem. Os detalhes destes métodos serão apresentados no curso de projeto e otimização aerodinâmica.
Existem vários métodos estocásticos, no entanto, dado que os Algoritmos Genéticos ou GA’s são os mais conhecidos, iremos abordar os principais conceitos destes otimizadores. Note que, o objetivo aqui não é apresentar tudo o que já foi publicado sobre estes algoritmos, mas de fornecer o mínimo de informações para que você possa conversar com proficiência com pessoas que atuam nesta área de conhecimento.
Algoritmos Genéticos utilizam os princípios de genética e seleção natural. Baseiam-se em leis probabilísticas para guiar o processo de busca. Isso não significa que são métodos adotam uma busca randômica da melhor solução. A solução do problema é representada por uma população que evolui durante o processo de otimização. Cada passo neste processo de otimização é conhecido pelo termo geração. Um algoritmo genético pode ser caracterizado pela seguinte sequência de operações:

Agora precisamos decodificar esta string para definirmos os valores decimais das variáveis de projeto. A decodificação é dada pela equação abaixo, onde precisamos ter a definição dos valores mínimos e máximos selecionados para a variável de projeto, o tamanho da string binária (neste caso 7) e a decodificação da string binária em valor decimal, DV(si).

Após a inserção destas informações na equação acima teremos o valor decimal da variável.
O processo de geração da população inicial (das strings binárias) pode ser feito de maneira randômica. No entanto, esta não é a maneira mais eficiente, pois podemos ter uma distribuição não homogênea da população. A figura abaixo mostra uma comparação quando geramos a população inicial usando o random ou o SOBOL, que consiste numa técnica de amostragem ou sampling.
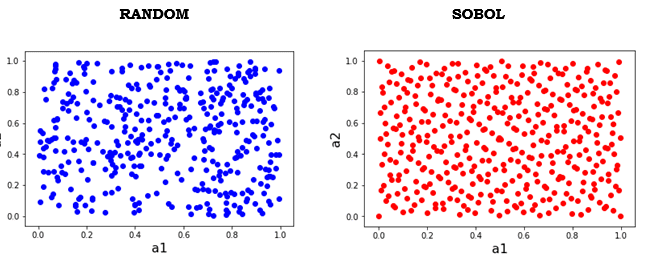
Cada par (a1,a2) consiste em um indivíduo inicial que será avaliado no próximo passo do algoritmo. Qual a principal diferença que você observa nestas duas figuras acima? Acredito que você também notou que o random não preenche o espaço de uma maneira homogênea.
Qual a implicação deste fato? Isso pode “atrasar” a obtenção da solução ótima, principalmente no caso onde se tem uma grande quantidade de variáveis de projeto.

O resultado da simulação será utilizado para atribuir algum valor para a função objetiva, sendo que, a função objetiva é a principal informação que o algoritmo genético utiliza para buscar a solução ótima.
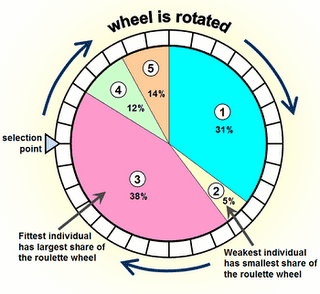
Uma delas usa o conceito de roleta. Neste conceito temos uma ‘roleta’ com o número de ‘slots’ igual da população da otimização (vide a figura a seguir). Indivíduos com maiores valores da função objetivo ganharão mais ‘slots’. Uma vez definida a disposição dos ‘slots’ da ‘roleta’ dá-se o processo de ‘rodar’ a roleta até extrairmos o número de indivíduos igual ao da população.
Do ponto de vista de implementação o conceito da roleta nada mais é do que um vetor onde cada indivíduo ganha uma quantidade de posições proporcional a sua função objetiva. O processo de ‘rodar’ a ‘roleta’ consiste em usar o random para selecionar um indivíduo neste vetor. Os indivíduos de maior função objetiva terão maior chance de serem selecionados uma vez que tem mais elementos no vetor.
O outro processo consiste no ‘mating pool’ que na verdade é um torneio. Como isso funciona? O primeiro passo consiste em definir o número de indivíduos que participarão do torneio. A seguir faz-se um sorteio para obter os indivíduos que serão “colocados” em uma “arena”. Note que o indivíduo de maior valor da função objetiva não terá necessariamente várias cópias na arena, como ocorre no método da roleta, pois o processo de escolha é randômico. Uma vez selecionados randomicamente estes indivíduos que irão para a “arena”, dá-se início ao processo de agrupar dois a dois os indivíduos e aquele que tiver maior função de mérito é o escolhido. Este processo tem que ser repetido até que você chegue ao número da população da sua otimização. A imagem abaixo mostra visualmente o conceito acima explicado.
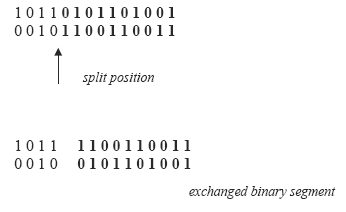
 A imagem abaixo mostra o resultado da aplicação destes operadores na população vigente do processo de otimização com o algoritmo genético.
A imagem abaixo mostra o resultado da aplicação destes operadores na população vigente do processo de otimização com o algoritmo genético.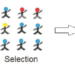 Estes operadores são típicos para os algoritmos que trabalham com problemas mono-objetivo. Já para problemas multi-objetivos, que são aqueles que possuem mais de uma função objetiva, existem alguns operadores adicionais como: ‘sharing-function’ e ‘non-domination’. Estes operadores não serão abordados aqui.
Estes operadores são típicos para os algoritmos que trabalham com problemas mono-objetivo. Já para problemas multi-objetivos, que são aqueles que possuem mais de uma função objetiva, existem alguns operadores adicionais como: ‘sharing-function’ e ‘non-domination’. Estes operadores não serão abordados aqui.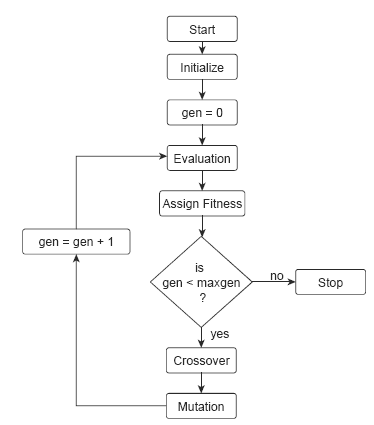 No próximo artigo será apresentado o estudo de otimização de um aerofólio e os códigos serão disponibilizados para os usuários. Então até o próximo artigo!
No próximo artigo será apresentado o estudo de otimização de um aerofólio e os códigos serão disponibilizados para os usuários. Então até o próximo artigo!O Portal tem diversos conteúdos para te ajudar a se qualificar para o mercado de trabalho. O que você está esperando?! Acesse agora e embarque com a gente nessa jornada do conhecimento:
▶ INSCREVA-SE no nosso canal do Youtube! Vem com a gente e embarque no mundo da aviação!
Siga a gente nas redes sociais!
▶ Instagram: @engenhariaaeronautica
Se transforme em um profissional disputado pelas principais empresas do mercado aeronáutico! A nova maneira de aprender engenharia e aplicar de fato os conhecimentos no mercado de trabalho! O Portal é formado por profissionais com vasta experiência no Mercado de Trabalho e com uma missão única: transmitir todo o conhecimento adquirido na indústria diretamente para o dia-a-dia do aluno! Todos os professores atuam em grandes empresas da aviação. Todo o conceito teórico é acompanhado de exemplos práticos que acontecem no dia-a-dia dos engenheiros. São mais de 15 especialistas prontos para trazer a experiência de anos na indústria aeronáutica para você.
O aluno de engenharia quer ter sucesso na indústria. Mas o que acontece quando existe uma distância infinita do que se ensina na faculdade para o que realmente é exigido no Mercado de Trabalho? O Portal é o caminho que vai te transformar em um engenheiro disputado pelas principais empresas do setor aeronáutico.